ОПРЕДЕЛЕНИЕ 2.2. ОКРУЖНОСТЬ ЭТО ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕКРАВНОУДАЛЁННЫХ ОТ ФИКСИРОВАНОЙ
ТОЧКИ НАЗЫВАЕМОЙ ЦЕНТРОМ.
УРАВНЕНИЕ ОКРУЖНОСТИ С ЦЕНТРОМ В ТОЧКЕ 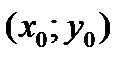 И РАДИУСА
И РАДИУСА 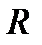 ХОРОШО ИЗВЕСТНО
ХОРОШО ИЗВЕСТНО
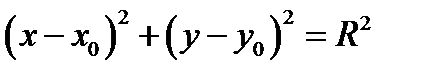 (2.5)
(2.5)
УПРАЖНЕНИЕ. ИСПОЛЬЗУЯ ГРАФИК, НАЙТИ КООРДИНАТЫ ЦЕНТРА ОКРУЖНОСТИ И ЕЁ РАДИУС (рис.5)
Рис.5
ЭЛЛИПС
ОПРЕДЕЛЕНИЕ 2.3. ЭЛЛИПС-ЭТО ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕК НА 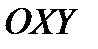 ПЛОСКОСТИ ТАКИХ, ЧТО
ПЛОСКОСТИ ТАКИХ, ЧТО
СУММА РАССТОЯНИЙ ИХ ДО ДВУХ ФИКСИРОВАННЫХ ТОЧЕК 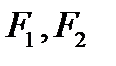 ЕСТЬ ВЕЛИЧИНА ПОСТОЯННАЯ.
ЕСТЬ ВЕЛИЧИНА ПОСТОЯННАЯ.
ТОЧКИ 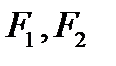 НАЗЫВАЮТСЯ ФОКУСАМИ ЭЛЛИПСА.
НАЗЫВАЮТСЯ ФОКУСАМИ ЭЛЛИПСА.
МЫ БУДЕМ РАССМАТРИВАТЬ «КАНОНИЧЕСКУЮ» СИСТЕМУ КООРДИНАТ, В КОТОРОЙ НАЧАЛО КООРДИНАТ ЯВЛЯЕТСЯ ЦЕНТРОМ СИММЕТРИИ ЭЛЛИПСА. КРОМЕ ТОГО ЭЛЛИПС СИММЕТРИЧЕН ОТНОСИТЕЛЬНО ОСЕЙ ТАКИХ КООРДИНАТ.
ПРИМЕР 2.3. НАЙТИ УРАВНЕНИЕ ГЕОМЕТРИЧЕСКОГО МЕСТА ТОЧЕК ПЛОСКОСТИ С КООРДИНАТАМИ 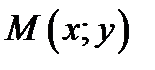 , ДЛЯ КОТОРЫХ СУММА РАССТОЯНИЙ ДО ДВУХ ТОЧЕК
, ДЛЯ КОТОРЫХ СУММА РАССТОЯНИЙ ДО ДВУХ ТОЧЕК 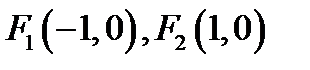 РАВНА 4.
РАВНА 4.
РЕШЕНИЕ. СОГЛАСНО ОПРЕДЕЛЕНИЮ 2.3. ИМЕЕМ:
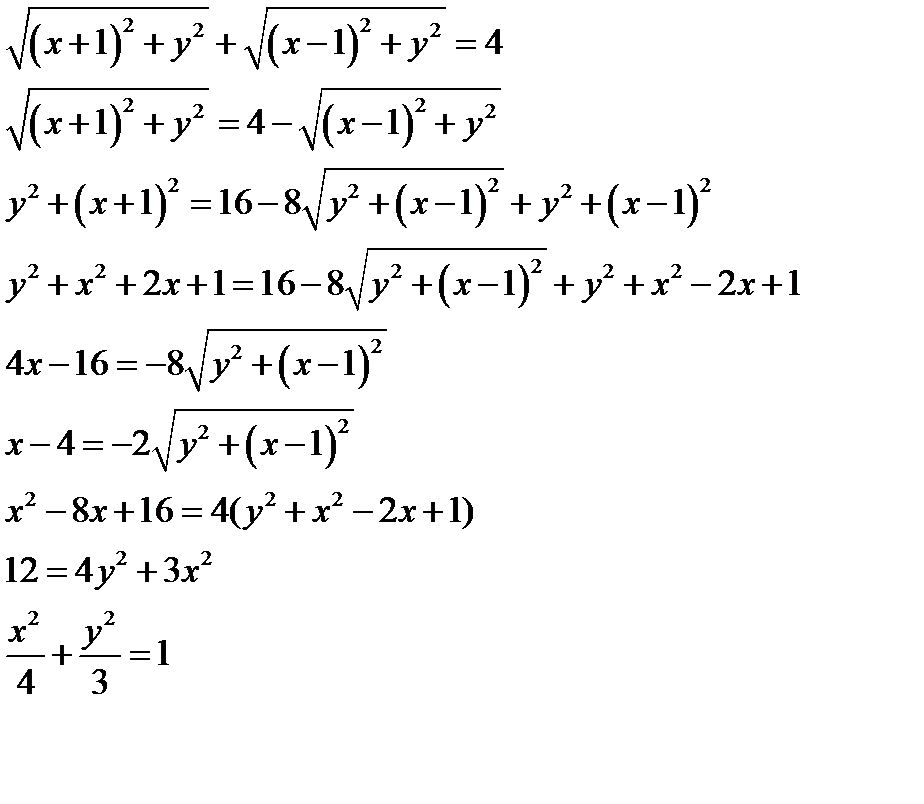
УРАВНЕНИЕ 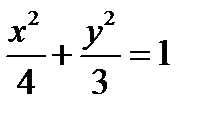 ЯВЛЯЕТСЯ КАНОНИЧЕСКИМ УРАВНЕНИЕМ ЭЛЛИПСА.
ЯВЛЯЕТСЯ КАНОНИЧЕСКИМ УРАВНЕНИЕМ ЭЛЛИПСА.
ОБЩИЙ СЛУЧАЙ СФОРМУЛИРОВАН В СЛЕДУЮЩЕЙ ТЕОРЕМЕ 2.3.
| P |
| F2 |
| F1 |
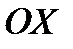 ПЛОСКОСТИ
ПЛОСКОСТИ 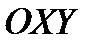 ЗАДАНЫ ФОКУСЫ ЭЛЛИПСА
ЗАДАНЫ ФОКУСЫ ЭЛЛИПСА 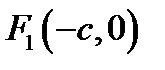 И
И 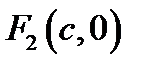 . СУММА РАССТОЯНИЙ ОТ ПРОИЗВОЛЬНОЙ ТОЧКИ
. СУММА РАССТОЯНИЙ ОТ ПРОИЗВОЛЬНОЙ ТОЧКИ 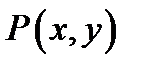 ЭЛЛИПСА ДО ФОКУСОВ РАВНА 2а. (а
ЭЛЛИПСА ДО ФОКУСОВ РАВНА 2а. (а 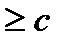
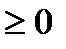 ). ТОГДА «КАНОНИЧЕСКОЕ» УРАВНЕНИЕ ЭЛЛИПСА ИМЕЕТ ВИД
). ТОГДА «КАНОНИЧЕСКОЕ» УРАВНЕНИЕ ЭЛЛИПСА ИМЕЕТ ВИД|
|
|
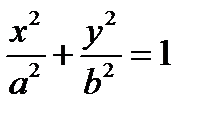 , (2.6)
, (2.6)
РИС.6 ГДЕ 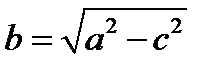 (2.7)
(2.7)
ЗАМЕЧАНИЕ. ФОКУСЫ ЭЛЛИПСА ЛЕЖАТ НА ОСИ 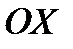 ТОГДА И ТОЛЬКО ТОГДА, КОГДА В УРАВНЕНИИ (2.6)
ТОГДА И ТОЛЬКО ТОГДА, КОГДА В УРАВНЕНИИ (2.6) 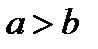 .
.
ОПРЕДЕЛЕНИЕ 2.4 ЭКСЦЕНТРИСИТЕТОМ ЭЛЛИПСА НАЗЫВАЕТСЯ ВЕЛИЧИНА 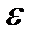 , КОТОРАЯ ВЫЧИСЛЯЕТСЯ ПО ФОРМУЛЕ
, КОТОРАЯ ВЫЧИСЛЯЕТСЯ ПО ФОРМУЛЕ
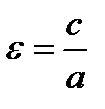 (2.8)
(2.8)
ТАК КАК У ЭЛЛИПСА  , ТО ЭКСЦЕНТРИСИТЕТ ЭЛЛИПСА ВСЕГДА МЕНЬШЕ ЕДИНИЦЫ. ЭКСЦЕНТРИСИТЕТ ЭЛЛИПСА ПОКАЗЫВАЕТ, НАСКОЛЬКО СИЛЬНО СПЛЮЩЕН ЭЛЛИПС К ПРЯМОЙ НА КОТОРОЙ ЛЕЖАТ ФОКУСЫ.
, ТО ЭКСЦЕНТРИСИТЕТ ЭЛЛИПСА ВСЕГДА МЕНЬШЕ ЕДИНИЦЫ. ЭКСЦЕНТРИСИТЕТ ЭЛЛИПСА ПОКАЗЫВАЕТ, НАСКОЛЬКО СИЛЬНО СПЛЮЩЕН ЭЛЛИПС К ПРЯМОЙ НА КОТОРОЙ ЛЕЖАТ ФОКУСЫ.
УПРАЖНЕНИЕ. ВЫБЕРИТЕ ПРАВИЛЬНЫЙ ОТВЕТ. ЧЕМ МЕНЬШЕ ЭКСЦЕНТРИСИТЕТ ЭЛЛИПСА, ТЕМ ЭЛЛИПС
1) БОЛЕЕ СПЛЮЩЕН 2) МЕНЕЕ СПЛЮЩЕН
ДИРЕКТРИСЫ ЭЛЛИПСА,ФОКУСЫ КОТОРОГО ЛЕЖАТ НА ОСИ 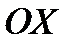 , ЗАДАЮТСЯ УРАВНЕНИЯМИ ВЕРТИКАЛЬНЫХ ПРЯМЫХ ЛИНИЙ
, ЗАДАЮТСЯ УРАВНЕНИЯМИ ВЕРТИКАЛЬНЫХ ПРЯМЫХ ЛИНИЙ
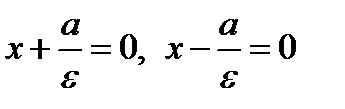 (2.9)
(2.9)
| M |
| D |
| F |
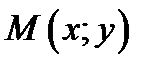 ДО ФОКУСА И ДО БЛИЖАЙШЕЙ К НЕМУ ДИРЕКТРИСЫ РАВНО ЧИСЛЕННОМУ ЗНАЧЕНИЮ ЭКСЦЕНТРИСИТЕТА (РИС.7)
ДО ФОКУСА И ДО БЛИЖАЙШЕЙ К НЕМУ ДИРЕКТРИСЫ РАВНО ЧИСЛЕННОМУ ЗНАЧЕНИЮ ЭКСЦЕНТРИСИТЕТА (РИС.7)
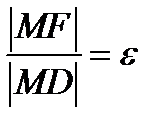 (2.10)
(2.10)
РИС.7
 2015-05-13
2015-05-13 439
439








