Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «КЕМЕРОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Кафедра автоматизации исследований
И технической кибернетики
Кемерово 2011
Составители: доцент Гутова С. Г., старший преподаватель Невзорова Т. А.
Дискретная математика: учеб.-метод. пособие/ ГОУ ВПО «Кемеровский государственный университет»; сост. С. Г. Гутова, Т. А. Невзорова. – Кемерово, 2011. – 128 с.
Учебно-методическое пособие разработано по курсу «Дискретная математика» для направлений «Прикладная математика и информатика», «Фундаментальная информатика и информационные технологии» в соответствии с требованиями ГОС ВПО и включает методические рекомендации
| Рекомендовано методической комиссией математического факультета «__»_________________2011 г. Председатель методической комиссии доцент _____________Л. Н. Фомина | Утверждено на заседании кафедры автоматизации исследований и технической кибернетики «__»______________2011 г. Заведующий кафедрой профессор ______________В. Я. Карташов |
Содержание
Глава 1. Теория множеств. Дискретная теория вероятности......5
1.1. Множества и операции над ними...................................................5
1.2. Векторы и прямые произведения множеств. Проекция вектора на ось......................................................................................................11
1.3. Комбинаторика...............................................................................14
1.4. Введение в дискретную теорию вероятностей...........................20
1.5. Соответствия и функции...............................................................29
1.6. Отношения......................................................................................35
1.7. Операции и алгебры......................................................................41
1.8. Гомоморфизм и изоморфизм алгебр............................................45
1.9. Полугруппы, группы, решетки.....................................................48
Глава 2. Теория графов.....................................................................53
2.1. Основные определения, способы задания, основные классы, изоморфизм графов..............................................................................53
2.2. Маршруты, цепи и циклы. Расстояния, диаметры, центры. Обходы. Разделяющие множества и разрезы.....................................63
2.3. Деревья, их свойства. Характеристические числа графов. Сети........................................................................................................70
Глава 3. Дискретные структуры: конечные автоматы, коды...76
3.1. Машина Тьюринга.........................................................................76
3.2. Основы теории кодирования........................................................80
Глава 4. Алгебра логических функций..........................................88
4.1. Основные определения..................................................................88
4.2. Эквивалентные преобразования...................................................91
4.3. Дизъюнктивные и конъюнктивные нормальные формы...........93
4.4. Дизъюнктивные нормальные формы и импликанты.................95
4.5. Минимизация ДНФ. Тупикова ДНФ...........................................98
4.6. Алгебра Жегалкина......................................................................103
4.7. Двойственность в алгебре логики. Самодвойственные функции...............................................................................................104
4.8. Функциональная полнота систем..............................................107
Глава 5. Логика высказываний и логика предикатов..............109
5.1. Логика высказываний..................................................................109
5.2. Логика предикатов.......................................................................117
Глава 6. Схемы переключателей. Комбинационные схемы...................................................................................................123
6.1. Схемы переключателей..............................................................123
6.2. Комбинационные схемы............................................................125
Список литературы
ГЛАВА 1. ТЕОРИЯ МНОЖЕСТВ.
ДИСКРЕТНАЯ ТЕОРИЯ ВЕРОЯТНОСТИ
Множества и операции над ними
Понятие множества является одним из основных первичных понятий математики. Множество – понятие неопределяемое.
Множество можно представить как совокупность некоторых объектов, объединенных по какому-либо признаку.
Множество состоит из элементов. В зависимости от их числа множества различают как конечные или бесконечные. Конечные множества могут состоять из одного или нескольких элементов.
Множество, не содержащее элементов, называется пустым множеством и обозначается Æ.
Множество обозначают заглавными буквами, а его элементы – прописными. Для записи множества используют фигурные скобки. Например, множество натуральных чисел от 3 до 10: М = {3, 4, 5, 6, 7, 8, 9, 10}.
Говоря об определенном множестве, мы полагаем, что для каждого объекта имеется две возможности: либо он входит в рассматриваемое множество, т.е. является его элементом, принадлежит ему (обозначается 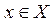 ); либо нет (обозначается
); либо нет (обозначается 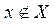 ).
).
Способы задания множества:
- перечисление всех элементов множества, например, множество однозначных неотрицательных чисел X = {0, 1, 2, 3, …, 9};
- указание общего свойства, которым обладают все элементы множества, например, множество четных натуральных чисел X = {2, 4, 6, 8, 10, 12, …} или X = { x: x = 2 n, 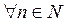 };
};
- рекуррентно, например: 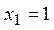 ,
, 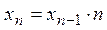 и др.
и др.
В математике приняты стандартные обозначения для некоторых числовых множеств: N – множество натуральных чисел, Z – множество целых чисел, Q – множество рациональных чисел, R – множество действительных чисел.
Множество А называют подмножеством множества В (обозначается 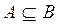 ), если каждый элемент множества А является также элементом множества В.
), если каждый элемент множества А является также элементом множества В.
Множества А и В называют равными (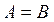 ), если каждый элемент множества А является одновременно элементом множества В и наоборот, т.е. если
), если каждый элемент множества А является одновременно элементом множества В и наоборот, т.е. если 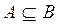 и
и 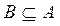 . Другими словами, два множества равны, если они состоят из одних и тех же элементов.
. Другими словами, два множества равны, если они состоят из одних и тех же элементов.
Множество I называется универсальным множеством (множество всех подмножеств) для некоторой системы множеств, если каждое множество этой системы является подмножеством I, т.е. { A, B, C, …}: 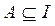 ,
, 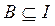 ,
, 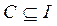 , …
, …
Дополнением множества А (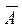 ) называется множество, состоящее из тех и только тех элементов универсального множества, которые не входят в множество А.
) называется множество, состоящее из тех и только тех элементов универсального множества, которые не входят в множество А.
Суммой (объединением) двух множеств А и В (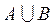 ) называется множество С, состоящее из тех элементов, которые принадлежат или множеству А, или В, или А и В одновременно.
) называется множество С, состоящее из тех элементов, которые принадлежат или множеству А, или В, или А и В одновременно.
Произведением (пересечением) двух множеств А и В (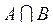 ) называется множество С, состоящее из тех и только тех элементов, которые принадлежат множествам А и В одновременно.
) называется множество С, состоящее из тех и только тех элементов, которые принадлежат множествам А и В одновременно.
Разностью двух множеств А и В (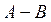 или
или 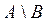 ) называется множество тех элементов множества А, которые не принадлежат множеству В:
) называется множество тех элементов множества А, которые не принадлежат множеству В:
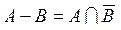 .
.
Свойства операций над множествами:
1) 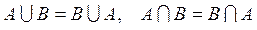 ;
;
2) 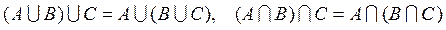 ;
;
3) 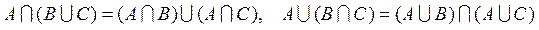 ;
;
4) 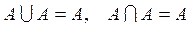 ;
;
5) 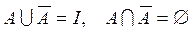 ;
;
6) 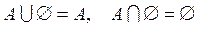 ;
;
7) 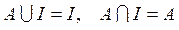 ;
;
8) 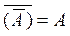 ;
;
9) 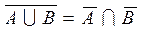 ,
, 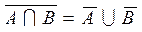 .
.
Прямым (декартовым) произведением двух множеств А и В (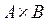 ) называется множество, состоящее из упорядоченных пар элементов, в которых первый элемент принадлежит множеству А, а второй – множеству В.
) называется множество, состоящее из упорядоченных пар элементов, в которых первый элемент принадлежит множеству А, а второй – множеству В.
Пример 1. Заданы два множества: А = {-2, -1, 0, 1, 2} и B = {0, 2, 4, 5}. Определить множества 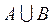 ;
; 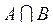 ;
; 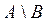 ;
; 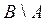 ;
; 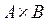 ;
; 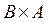 и их мощность.
и их мощность.
Решение:
Множество А = {-2, -1, 0, 1, 2} состоит из пяти элементов, следовательно мощность этого множества равна 5: 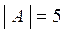 .
.
Аналогично, B = {0, 2, 4, 5} содержит четыре элемента: 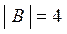 .
.
Для наглядности, в перечислении элементов заданных множеств выделим жирным курсивом повторяющиеся (общие) элементы:
А = {-2, -1, 0, 1, 2 } и B = { 0, 2, 4, 5}.
По определению пересечение двух множеств состоит только из общих для обоих множеств элементов, следовательно, 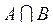 = {0, 2} и
= {0, 2} и 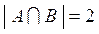 .
.
По определению объединение двух множеств состоит из всех элементов, которые принадлежат и множеству А, и множеству В, следовательно, 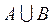 = {-2, -1, 0, 1, 2, 4, 5} и
= {-2, -1, 0, 1, 2, 4, 5} и 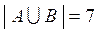 или по правилу суммы
или по правилу суммы 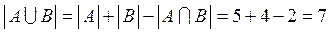 .
.
Множество 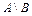 является разностью двух множеств А и В и состоит из элементов множества А, которые одновременно не принадлежат множеству В, следовательно
является разностью двух множеств А и В и состоит из элементов множества А, которые одновременно не принадлежат множеству В, следовательно 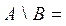
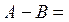 {-2, -1, 1} и
{-2, -1, 1} и 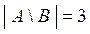 .
.
Аналогично, 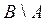
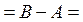 {4, 5} и
{4, 5} и 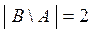 .
.
Прямое (декартово) произведение:
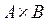 = {(-2, 0); (-2, 2); (-2, 4); (-2, 5); (-1, 0); (-1, 2); (-1, 4); (-1, 5);
= {(-2, 0); (-2, 2); (-2, 4); (-2, 5); (-1, 0); (-1, 2); (-1, 4); (-1, 5);
(0, 0); (0, 2); (0, 4); (0, 5); (1, 0); (1, 2); (1, 4); (1, 5); (2, 0); (2, 2); (2, 4); (2, 5)}
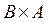 = {(0, -2); (0, -1); (0, 0); (0, 1); (0, 2); (2, -2); (2, -1); (2, 0); (2, 1); (2, 2); (4, -2); (4, -1); (4, 0); (4, 1); (4, 2); (5, -2); (5, -1); (5, 0); (5, 1); (5, 2)}
= {(0, -2); (0, -1); (0, 0); (0, 1); (0, 2); (2, -2); (2, -1); (2, 0); (2, 1); (2, 2); (4, -2); (4, -1); (4, 0); (4, 1); (4, 2); (5, -2); (5, -1); (5, 0); (5, 1); (5, 2)}
Из этого примера видно, что 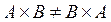 , но при этом
, но при этом 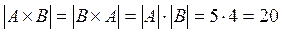 .
.
Пример 2. Заданы множества, являющиеся промежутками числовой оси А = [-2.8; 0)и B = [-2; 0]. Определить 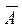 ;
; 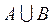 ;
; 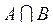 ;
; 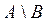 ;
; 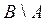 .
.
По определению, дополнением множества А называется множество, состоящее из тех и только тех элементов универсального множества, которые не входят в множество А. Для числовых промежутков универсальным множеством (множеством всех подмножеств-промежутков) является вся числовая ось 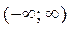 .
.
Следовательно, 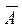 =
= 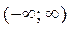 - [-2,8; 0) =
- [-2,8; 0) = 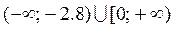 .
.
Далее, для наглядности определения множеств 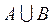 ;
; 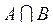 ;
; 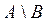 и
и 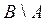 изобразим (схематично) расположение заданных промежутков относительно друг друга:
изобразим (схематично) расположение заданных промежутков относительно друг друга:
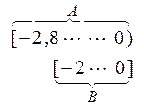
По определению объединение двух множеств состоит из всех элементов, которые принадлежат и множеству А, и множеству В, следовательно 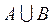 =
= 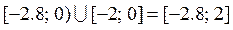 .
.
По определению пересечение двух множеств состоит только из общих для обоих множеств элементов, следовательно,
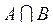 =
= 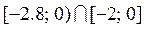
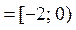 .
.
Множество 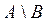 является разностью двух множеств А и В и состоит из элементов множества А, которые одновременно не принадлежат множеству В, следовательно,
является разностью двух множеств А и В и состоит из элементов множества А, которые одновременно не принадлежат множеству В, следовательно, 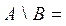
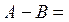 =
= 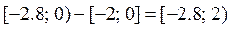 .
.
Множество 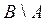 , по определению, состоит из элементов множества В, которые одновременно не принадлежат множеству А, а таким элементом является единственное число 0, и, следовательно разностью промежутков В и А является конечное множество, состоящее из одного единственного элемента:
, по определению, состоит из элементов множества В, которые одновременно не принадлежат множеству А, а таким элементом является единственное число 0, и, следовательно разностью промежутков В и А является конечное множество, состоящее из одного единственного элемента: 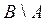
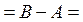
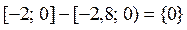 .
.
 2015-04-01
2015-04-01 798
798







