2015-05-13
567
Пусть дана выборка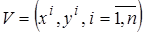 
из статистически независимых наблюдений значений 
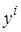неизвестной однозначной зависимости 
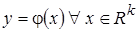(3.19) и её аргументов 
.
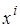Считается, что функция (3.19) и плотности вероятности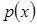 
, 
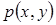в области определения 
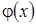непрерывные и достаточно гладкие.
Идея предлагаемого подхода состоит в декомпозиции исходной задачи, построении семейства локальных решающих функций на основании однородных частей обучающей выборки и последующей их организации в едином нелинейном решающем правиле с помощью методов непараметрической статистики. Однородная часть обучающей выборки содержит её элементы, удовлетворяющие одному или нескольким требованиям, таким как наличие однотипных признаков (непрерывные, дискретные, лингвистические и др.), отсутствие либо наличие пропусков данных, что порождает широкий круг условий синтеза непараметрических решающих правил. Однородные части обучающей выборки могут отличаться размерностью и количеством элементов.
На основании однородных частей обучающей выборки сформируем наборы признаков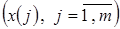 
из исходных 
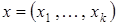и построим семейство частных моделей 
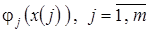на основании обучающих выборок 
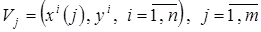. Интеграция частных моделей в нелинейном коллективе решающих правил осуществляется в соответствии с процедурой
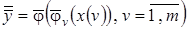, (3.32)
где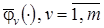 
, 
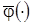- модели частных зависимостей 
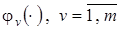и объединяющего их нелинейного оператора 
.
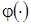Структура предлагаемого коллектива решающих правил при восстановлении многомерной стохастической зависимости (3.19) представлена на рис. 3.8.
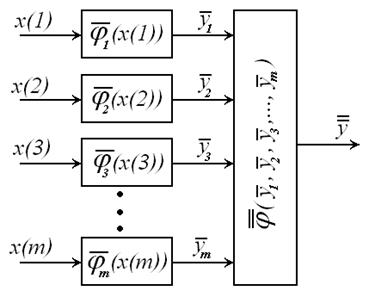
Рис. 3.8. Нелинейный непараметрический коллектив решающих правил (3.32)
с каскадной структурой
При построении частных моделей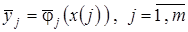 
могут быть использованы известные методы аппроксимации, включая непараметрическую регрессию
, 
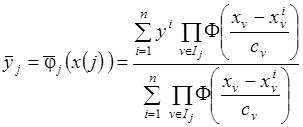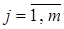, (3.33)
где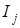 
- номера признаков, составляющих их набор 
; 
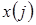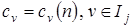- коэффициенты размытости ядерных функций, значения которых зависят от объёма выборки 
.
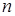Обобщение частных моделей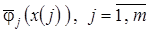 
в едином решающем правиле осуществляется с помощью непараметрической статистики
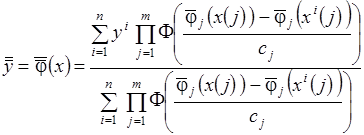, (3.34)
формируемой по выборке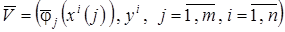 
.
Оптимизация непараметрического коллектива (3.34) по коэффициентам размытости ядерных функций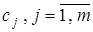 
производится в режиме «скользящего экзамена» из условия минимума эмпирического критерия
.
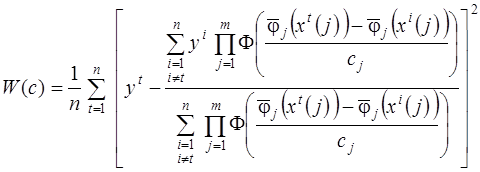Преимущества предлагаемой процедуры по сравнению с моделями типа «черный ящик» состоит в возможности учета частичных априорных сведений о виде взаимосвязи между переменными исследуемой зависимости и «обходе» проблем малых выборок за счет снижения размерности задачи.
