2015-05-13
2306
Уравнение и передаточная функция звена имеют вид
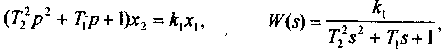
причем предполагается, что T1>=2T2 так как при этом корни характеристического уравнения
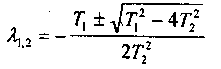
будут вещественными. Передаточную функцию апериодического звена второго порядка можно записать в виде
где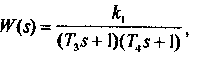 
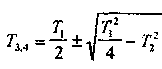
Амплитудно-фазовая частотная характеристика звена:
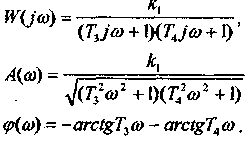
Логарифмическая амплитудная частотная характеристика звена:
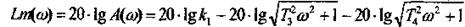
При (T1<2T2) звено переходит в колебательное (см. ниже) состояние, поэтому постоянная Т1, определяющая инерционность звена, является в то же время демпфирующим фактором (увеличение Т1 приводит к отсутствию колебаний). Переходная и весовая функции аналогично предыдущему имеют вид
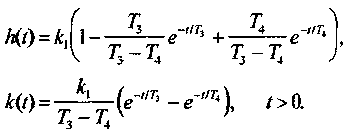
Примерами такого звена являются: а) двигатель постоянного тока при учете инерционности цепи якоря; б) электро машинный усилитель; в) двойная цепочка LR.
Уравнение и передаточная функция звена:
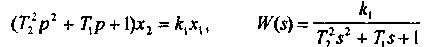
причем предполагается T1<2T2, так что корни характеристического уравнения - комплексные. Общепринята запись передаточной функции колебательного звена в виде
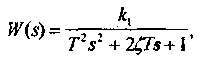
где Т=Тг,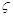 
=T1/(2T2), причем 0< 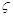< 1, так как при 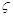= > 1 звено становится апериодическим второго порядка.
Амплитудно-фазовая частотная характеристика звена:
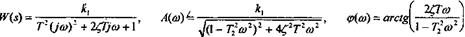
Амплитудная характеристика уменьшается с увеличением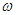 
, т.е. A(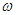) < k1, если 1> 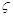>0.707. При 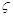<0.707 появляется "горб" на характеристике A(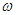), который уходит в бесконечность при) 
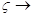0. Поэтому величина 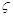,=T1/(2T2) называется параметром затухания. Отсюда видна роль
постоянных времени T1 и Т2 в уравнении звена: постоянная T1 "раскачивает" колебания, а T2 - "демпфирует" их.
Логарифмическая амплитудная частотная характеристика звена
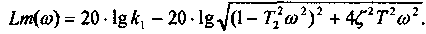
Переходная и весовая функции колебательного звена соответственно имеют вид
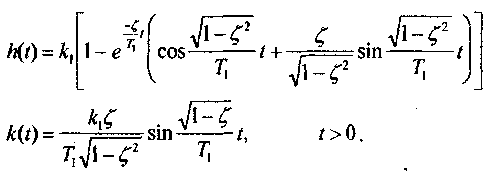
При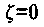 
колебания становятся незатухающими, а при 
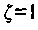колебания вырождаются в апериодический процесс.
Пример колебательного звена - на рис. 1.2.
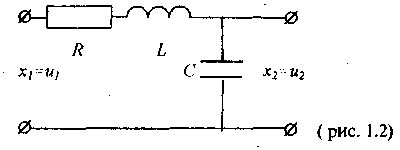
Частный случай колебательного звена, при 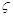=0, когда h(t) и k(t) становятся незатухающими (периодическими), носит название консервативного звена.
