Гармонических сигналов

Цель работы

Экспериментальное исследование условий, при которых обеспечивается ортогональность гармонических сигналов.

Краткая характеристика исследуемых цепей и сигналов

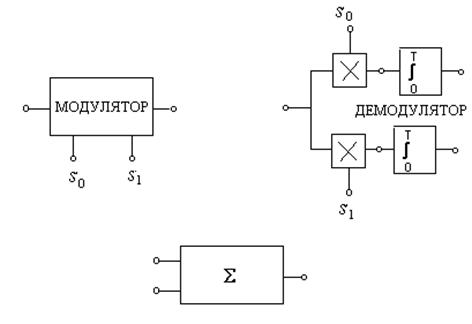
В работе используется универсальный лабораторный стенд со сменным блоком «МОДУЛЯТОР – ДЕМОДУЛЯТОР», схема и описание которого приведены в работе 20 (рис. 20.1). В данной работе используется только часть схемы демодулятора, а именно блоки перемножителя и интегратора, которые вычисляют скалярное произведение сигналов, подаваемых на входы перемножителя за время Т = 450 мкс (длительность символа):

.

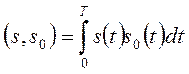Здесь s (t) – исследуемый сигнал на входе демодулятора, а s ₀(t) – эталонный сигнал, соответствующий символу «0» при выбранном виде модуляции. Оценка ортогональности производится по выходному сигналу интегратора в момент окончания символа. При полной ортогональности исследуемого и эталонного сигналов на выходе интегратора сигнал отсутствует.

В качестве исследуемых сигналов s (t) используются гармонические сигналы с разными частотами, а также их смесь. Эталонные сигналы s ₀ и s ₁, подаваемые на перемножители демодулятора, зависят от положения переключателя ВИД МОДУЛЯЦИИ, расположенного над обозначением МОДУЛЯТОРА. Для ЧМ эти сигналы соответствуют: s ₀ (для символа «0») – гармоническому сигналу с частотой f ₁=18 кГц, а s ₁ (для символа «1») f ₂=27 кГц. Для АМ s ₀(t)=0, а s ₁(t) – такой же сигнал, как и при ЧМ. Источниками исследуемых сигналов s ₀ и s ₁ являются гнезда, расположенные ниже обозначения МОДУЛЯТОРА.

В качестве измерительных приборов используются: встроенный звуковой генератор (ЗГ), встроенный вольтметр переменного напряжения и двухлучевой осциллограф.

Домашнее задание

Изучить раздел курса «Ортогональность сигналов и разделение сигналов по форме» по конспекту лекций и литературе:

[3, с. 54–66; 4, с. 30–36; 5, с. 23 –34; 6, с. 26–30].

Лабораторное задание

Исследовать ортогональность гармонических сигналов с различными частотными и фазовыми соотношениями.

Методические указания

1. Установить переключатель вида модуляции в положение ЧМ. Подключить сигнал s ₀ со входа МОДУЛЯТОРА на вход ДЕМОДУЛЯТОРА (рис. 19.1).

Зарисовать осциллограммы:

· на входе ДЕМОДУЛЯТОРА. Отрегулировать масштаб изображения по оси времени так, чтобы на экране укладывалось 10–12 периодов сигнала и в дальнейшем масштаб не менять;

· на выходах перемножителей верхней и нижней ветвей ДЕМОДУЛЯТОРА (в одном масштабе по вертикальной оси);

·

на выходах интеграторов обеих ветвей (также в одном масштабе).

Рис. 19.1. Схема для измерения скалярного произведения сигналов

2. По последним осциллограммам оценить скалярные произведения сигналов (в делениях по вертикали относительно нуля в момент окончания символа) для сигналов:

· s ₀(t) и s ₀(t);

· s ₀(t) и s ₁(t).

Этот момент легко определить по вертикальному скачку на осциллограмме верхнего интегратора. Для определения положения нуля напряжения на осциллограмме (т. е. положения оси времени) следует закоротить вход осциллографа.

3. Повторить п.1 для сигнала s ₁(t) на входе ДЕМОДУЛЯТОРА, фиксируя только осциллограммы на выходах интеграторов.

Оценить скалярные произведения сигналов:

· s ₁(t) и s ₀(t);

· s ₁(t) и s ₁(t).

4. Подать на вход ДЕМОДУЛЯТОРА сумму сигналов s ₀(t) + s ₁(t), используя сумматор стенда. Оценить скалярные произведения сигналов:

· (s ₀ + s ₁) и s ₀;

· (s ₀ + s ₁) и s ₁.

Поочередно отключая один из входных сигналов сумматора, зафиксировать в отчете изменения в сигналах на выходах интеграторов.

5. Установить вид модуляции – АМ. При этом работает только нижняя ветвь ДЕМОДУЛЯТОРА, так как s ₀(t)=0. Отключить сигнал s₀ от входа сумматора, а s ₁ сохранить на втором входе сумматора. Регулятором вертикального отклонения осциллографа, подключенного к выходу сумматора, установить размах синусоиды (сигнала s ₁) – 4 клетки, что соответствует амплитуде s ₁: a = 2 клетки. Подключив к другому входу сумматора генератор шума и, отключив от сумматора s ₁, регулятором выхода ГШ (не трогая настройки осциллографа!) получить на экране ширину шумовой дорожки 6 клеток, что согласно «правилу трех сигма» для нормального закона соответствует 6s = 6 клеток, т.е. s = 1 клетка. Восстановив сигнал s₁ на входе сумматора, получим на его выходе соотношение a /s = 2. Наблюдая осциллограммы на выходе нижнего интегратора, оценить скалярное произведение сигналов:

· s ₁(t)+ n (t) и s ₁(t); отключая источник шума от входа сумматора, оценить влияние шума на величину скалярного произведения;

· n (t) и s ₁(t); для этого отключить от входа сумматора s ₁(t).

6. Сохраняя прежний режим работы МОДУЛЯТОРА (АМ), подать от встроенного ЗГ гармонический сигнал с частотой 27 кГц и напряжением около 1,5 В на вход ДЕМОДУЛЯТОРА. Подстраивая частоту ЗГ, добиться максимального отклика нижнего интегратора. Попытаться «остановить» осциллограмму более тщательной установкой частоты ЗГ. Далее, не перестраивая ЗГ, примерно в течение минуты наблюдать за величиной максимума отклика интегратора, после чего повторить измерение. Вновь подстроить ЗГ, добиваясь максимума. Объяснить причину изменения скалярного произведения двух гармонических сигналов, полученных от разных генераторов.

7. Сохраняя условия п. 6, перестраивать ЗГ в пределах 15–35 кГц с шагом в 5 кГц, фиксируя в табл. 19.1 величину максимума отклика интегратора в зависимости от частоты.

Таблица 19.1

Величина скалярного произведения сигналов в зависимости от сдвига частот

F зг	кГц		…	…	…
U max интегр	дел

8. Установить вид модуляции – ФМ. Подать сигнал s ₀ от нижнего входа МОДУЛЯТОРА на вход ДЕМОДУЛЯТОРА. Входы двухлучевого осциллографа подключить к выходам интеграторов. Зафиксировать осциллограммы на выходах интеграторов, оценив величины и знаки (полярности) скалярных произведений сигналов:

· s ₀(t) и s ₁(t);

· s ₀(t) и s ₀(t).

Отчет

Отчет должен содержать:

1) результаты исследований по всем пунктам, выводы и график по данным табл. 19.1;

2) вывод (в каждом пункте отчета) о том, чем отличались (либо не отличались) сигналы-сомножители скалярных произведений.

Контрольные вопросы

1. Какие способы представления сигналов Вам известны?

2. С какой целью введено понятие многомерного пространства?

3. Какое пространство называют

· линейным;

· метрическим;

· евклидовым?

4. Каков смысл понятий «норма» и «расстояние» в применении к сигналам?

5. Какой смысл имеет понятие «скалярное произведение» в применении к сигналам.

6. От чего зависит угол между векторами, отображающими сигналы в многомерном пространстве?

7. Как Вы представляете себе ортогональные сигналы (приведите несколько примеров).

8. От каких параметров зависит скалярное произведение гармонических сигналов?

9. Какую роль может играть начальная фаза одного из гармонических сигналов в оценке их скалярного произведения?

10. Какую роль в оценке ортогональности сигналов играет время интегрирования (Т)?

11. Как с помощью понятия «расстояние» можно оценить помехоустойчивость системы связи?

Лабораторная работа 20