Матричные уравнения

На практике часто встречаются различные матричные уравнения. Например, рассмотрим уравнение

ABXC = D,

где A, B, C – невырожденные матрицы. Преобразуя это уравнение, получим

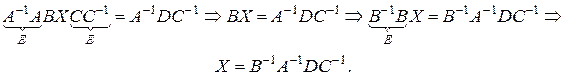
Если хотя бы одна из матриц А, В, С окажется вырожденной, то изложенный способ будет непригоден. В этом случае матричное уравнение или имеет бесконечно много решений, или вообще не имеет решений.

Пример 3.3. Решить матричное уравнение

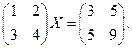
Решение. Данное уравнение коротко можно записать следующим образом: AX=B. Тогда решение будет иметь вид X=A ^–1B, т.е.

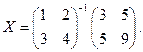
Поскольку 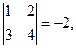то 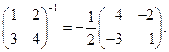Следовательно,

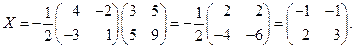. à