| Математическое ожидание | Дисперсия | |||
| ДСВ | 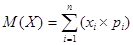 | 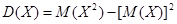 , где , где 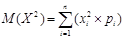 | ||
| НСВ | 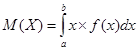 | 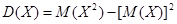 , где , где 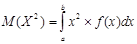 | ||
| ДСВ НСВ | 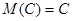 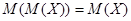 | 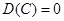 | ||
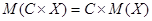 | 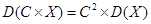 | |||
| 3а | 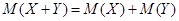 | 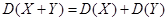 | ||
| 3б | 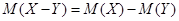 |  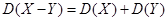 | ||
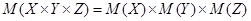 где где 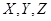 – независимые – независимые | 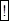 | |||
Среднее квадратическое отклонение 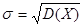 | ||||
Пояснения свойств математического ожидания (устно).
Названия и числовые характеристики некоторых
распределений дискретных случайных величин
Схема Бернулли, Биномиальное распределение, Рn(к)= 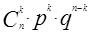 . . | М(Х)= 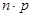 | D(X)= 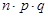 |
Геометрическое распределение, Р(к)= 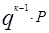 | М(Х)= 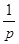 | D(X)= 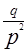 |
Распределение Пуассона, Рn(к)= 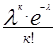 , , 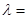 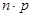 | М(Х)= 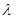 | D(X)= 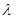 |
Решение задач
Пример 1. «Страховая компания». Согласно американским статистическим таблицам смертности, вероятность того, что 25-летний человек проживет еще год равна 0,992 (следовательно, вероятность того, что он умрет, равна 0,008). Страховая компания предлагает такому человеку застраховать свою жизнь на год на сумму 1000$. Страховой взнос составляет 10$. Найти математическое ожидание прибыли страховой компании.
Решение. Если, по истечении года, человек остается живым, а это происходит с вероятностью 0,992, то страховая компания получит доход +10$. Если же, по истечении года, человек умрет или погибнет, а это происходит с вероятностью 0,008, то вступает в силу фраза о том, что «страховая компания выплачивает 1000$». Однако на самом деле здесь скрыто то, что компания несет убытки не в тысячу долларов, а в 990$, так как человек уже отдал 10$ в страховую компанию.
Составим закон распределения вероятностей
| Х | +10 | -990 |
| р | 0,992 | 0,008 |
Найдем математическое ожидание
М(Х)= 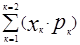 =10*0.992+(-990)*0,008=+2.
=10*0.992+(-990)*0,008=+2.
Таким образом, с каждого застрахованного компания имеет доход два доллара. Накапливая такие доходы, компания может оплачивать труд своим страховым агентам и развиваться.
Пример 2. «Игра в рулетку». На колесе рулетки имеется 38 одинаково расположенных гнезд, которые нумеруются так: 00, 0, 1, 2, ….36. Игрок может поставить один доллар на любой номер. Если его номер выиграл, игрок получает 36$. Найти математическое ожидание выигрыша игрока.
Решение. Так как ни одному из гнезд не отдается предпочтение при броске шарика в рулетку, то события, состоящие в появлении конкретного гнезда, равновероятны. А, так как они образуют полную группу событий, то сумма таких одинаковых вероятностей равна единице, и, следовательно, каждое гнездо может появиться с вероятностью 1/38 (а не 1/36, как это может показаться на первый взгляд!)
Если игрок не угадывает выпавший номер, то он несет убыток в один доллар, а такое происходит в 37 случаях из 38, причем это события несовместные, и по теореме о вероятности суммы несовместных событий вероятность потери доллара оказывается раной 37/38. В случае угадывания номера игрок получает 36, а на самом деле лишь 35 долларов, так как уже один доллар отдал игровому дому, и такое происходит с вероятностью 1-37/38=1/38 (выигрыш это событие противоположное проигрышу).
Составим закон распределения вероятностей дискретной случайной величины Х – выигрыш игрока.
| Х | -1 | +35 |
| р | 37/38 | 1/38 |
Найдем математическое ожидание
М(Х)= 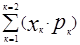 =(-1)*(37/38)+(+35)*(1/38)=-1/19.
=(-1)*(37/38)+(+35)*(1/38)=-1/19.
Таким образом, игра не является «справедливой». Игрок будет терпеь убытки, а игорный дом обеспечивает себе средний доход и часть дохода затрачивает на накладные расходы, и т.д.
Сосчитаем дисперсию D(Х) и среднее квадратическое отклонение 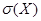 .
.
D(Х)=М(Х2)-[М(Х)]2 =(-1)2*(37/38)+(+35)2*(1/38)-(-1/19)2=35.07,
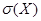 =
= 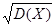 =5.9
=5.9
То есть, выигрыши (и проигрыши) игроков разбросаны (в среднем) между (-1/19-5.9) и (-1/19+5,9), а отдельные «получения 36долларов» служат приманкой к игре новых игроков.
Определение. Величину называют случайной, если в результате испытания она примет лишь одно возможное значение, заранее не известное и зависящее от случайных причин (с.в. или СВ).
С.в. обозначаются заглавными латинскими буквами X, Y, Z, а их возможные значения соответствующими строчными буквами x, y, z.
Примеры случайных величин:
1. число мальчиков среди 100 новорожденных;
2. время ожидания автобуса на остановке;
3. оценка, полученная на экзамене;
4. отклонение диаметра детали от стандарта и т.д.
Чтобы задать случайную величину, необходимо указать ее возможные значения и вероятности.
По типу принимаемых значений с.в. делятся на дискретные и непрерывные.
Определение. Случайная величина, принимающая отдельные возможные значения с определенными вероятностями, называется дискретной случайной величиной (д.с.в. или ДСВ).
Определение. Непрерывной называется случайная величина, которая может принимать все значения из некоторого промежутка (н.с.в. или НСВ).
Вероятностная характеристика с.в. может быть задана с помощью функции распределения.
Определение. Вероятность того, что случайная величина примет значение, меньше x, называется функцией распределения 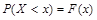 .
.
Свойства функции распределения:
1. 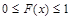 ;
;
2. 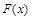 - неубывающая функция; если
- неубывающая функция; если 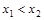 , то
, то 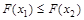 ;
;
3. 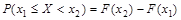 ;
;
4. 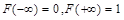 .
.
 2015-05-13
2015-05-13 2829
2829
