Дискретные случайные величины. Определение. Соответствие между отдельными возможными значениями и их вероятностями называется законом распределения дискретной случайной величины. X

Определение. Соответствие между отдельными возможными значениями и их вероятностями называется законом распределения дискретной случайной величины.

X	x₁	x₂	...	x_n
p	p₁	p₂	...	p_n

Поскольку в одном испытании д.с.в. принимает только одно возможное значение, то события 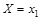, ,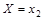..., 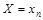образуют полную группу, то есть сумма их вероятностей равна единице:

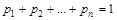Если множество возможных значений д.с.в. X бесконечно, то соответствующий ряд вероятностей сходится, а его сумма равна единице: .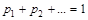

Закон распределения д.с.в. можно изобразить графически. Для этого в прямоугольной системе координат строят точки 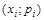, а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.

Пример 1. Монету подбрасывают 2 раза. Найти закон распределения и функцию распределения д.с.в. X – числа выпавших “гербов”. Найти вероятность того, что герб выпадет не менее 1 раза.

При двух подбрасываниях может выпасть 0, 1 или 2 “герба”. Вероятности этих событий можно определить по формуле Бернулли с параметрами n=2, p=0.5.

X
p	0.25	0.5	0.25

;

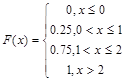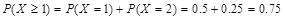
Примеры дискретных распределений:

1. Вырожденное: 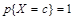, где c – константа.

2. Дискретное равномерное:

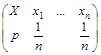
3. Распределение Бернулли:

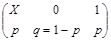
4. Биномиальное распределение с параметрами (n,p): случайная величина принимает целые значения от 0 до n, а их вероятности определяются по формуле Бернулли: 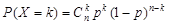. Случайная величина с таким распределением имеет смысл числа успехов в схеме Бернулли с числом испытаний n.

Пример 2. Банк выдает 5 кредитов. Вероятность не возврата кредита равна 0.2 для каждого из заемщиков. Составить таблицу для закона распределения количества заемщиков, не вернувших кредит по окончании срока кредитования.

Так как заемщики действуют независимо, то выдачу кредитов можно рассматривать как 5 независимых событий. Вероятность не возврата k кредитов определяется биномиальным распределением с параметрами n=5, p=0.2, q=1-0.2=0.8.

X
p	0.32768	0.4096	0.2048	0.0512	0.0064	0.00032

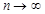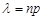5. Распределение Пуассона с параметром l>0: данная случайная величина является приближением схемы Бернулли при , а . Вероятности значений случайной величины находятся по формуле Пуассона: .

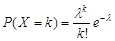Пример 3. На базу отправлено 10 000 изделий. Вероятность того, что в пути изделие получит повреждение, равна 0.0003. Найти вероятность того, что на базу прибудут 4 поврежденных изделия.

По условию задачи n=10 000, p=0.0003, k=4. Находим .

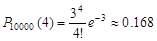
6. Геометрическое распределение: Случайная величина принимает целые значения 1,2,... с вероятностями 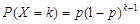. Случайная величина с таким распределением имеет смысл номера первого успешного испытания в схеме Бернулли с вероятностью p.

Пример 4. Каждый десятый посетитель автосалона, к которому подходит продавец-консультант, покупает автомобиль. Найти вероятность того, что третий посетитель автосалона, к которому подошел продавец, уедет на новом автомобиле.

По условию задачи p=0.1, k=3.

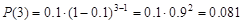
7. Гипергеометрическое распределение: д.с.в. X имеет гипергеометрическое распределение с параметрами n, N и K, если X принимает целые значения от 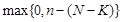до 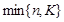с вероятностями 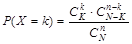. Случайная величина с таким распределением имеет смысл числа белых шаров среди n шаров, выбранных наудачу и без возвращения из урны, содержащей K белых и N‑K не белых шаров.

Пример 5. В партии из 10 кинескопов 2 кинескопа бракованные. Было реализовано 3 кинескопа. Найти закон распределения д.с.в. X – числа бракованных кинескопов среди реализованных.

Случайная величина X имеет гипергеометрическое распределение с параметрами N=10 (общее число кинескопов), K=2 (число бракованных кинескопов), n=3 (число реализованных кинескопов). Закон распределения представлен в виде таблицы: