Чтобы однозначно задать н.с.в., необходимо указать ее функцию распределения.
Определение. Случайную величину называют непрерывной, если ее функция распределения есть непрерывная функция с непрерывной производной.
Вероятность того, что н.с.в. примет значение из некоторого интервала, определяется формулой: 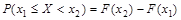 .
.
Вероятность того, что непрерывная случайная величина примет некоторое конкретное значение равна нулю: 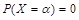 . . |
Поскольку вероятность того, что н.с.в. примет конкретное значение, справедливо следующее равенство:
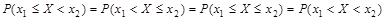 .
.
Пример 1. Н.с.в. X задана функцией распределения 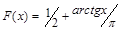 . Найти вероятность того, что величина X примет значение, заключенное в интервале (0;1).
. Найти вероятность того, что величина X примет значение, заключенное в интервале (0;1).
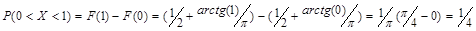 .
.
Определение. Производная от функции распределения непрерывной случайной величины X называется плотностью распределения вероятностей X: 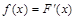 .
.
Связь между функцией распределения и плотностью распределения: 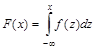
Свойства плотности распределения:
1. 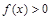 ;
;
2. 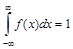 (условие нормированности);
(условие нормированности);
3. если все возможные значения н.с.в. лежат внутри интервала (a;b), то 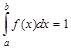 ;
;
4. вероятность того, что н.с.в. примет значение из некоторого интервала, равна 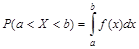 .
.
Пример 2. Н.с.в. X задана плотностью распределения 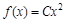 на интервале
на интервале 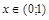 . Найти константу C и вероятность того, что величина X примет значение, заключенное в интервале (0;0.5) и (0;2).
. Найти константу C и вероятность того, что величина X примет значение, заключенное в интервале (0;0.5) и (0;2).
Исходя из условия нормированности н.с.в. 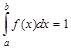 .
.
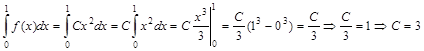 .
.
 2015-05-13
2015-05-13 759
759








