Под индексом понимается относительная величина, показывающая, во сколько раз уровень изучаемого явления в данных условиях отличается от уровня того же явления в других условиях. Различие условий может проявляться:
· во времени (индексыдинамики),
· в пространстве (территориальные индексы),
· в выборе в качестве базы сравнения планового показателя (индекс планового задания) или уровня договорных обязательств (индекс выполнения обязательств).
Показатель, изменение которого характеризуется индексом, называют индексируемойвеличиной (так, например, в индексе цен индексируемой величиной является цена, в индексе заработной платы - заработная плата, в индексе физического объёма продукции - объём выпуска в натуральном выражении). По виду индексируемой величины различают индексы объёмных и качественных показателей. Объёмные индексы служат для измерения изменения объёмных показателей, выраженных абсолютными величинами (например, объём выпуска продукции, численность работающих). Качественные индексы служат для измерения изменения качественных показателей, определяемых в расчете на единицу (например, цена или себестоимость единицы продукции, производительность труда).
Обычно используются следующие обозначения индексируемых величин:
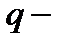 количество (объём) какого-либо товара, продукции в натуральном выражении;
количество (объём) какого-либо товара, продукции в натуральном выражении;
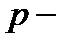 цена единицы товара;
цена единицы товара;
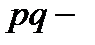 стоимость продукции, или товарооборот;
стоимость продукции, или товарооборот;
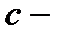 себестоимость единицы продукции;
себестоимость единицы продукции;
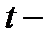 затраты времени на производство единицы продукции, трудоёмкость;
затраты времени на производство единицы продукции, трудоёмкость;
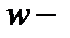 производительность труда, т.е. выработка продукции в единицу времени или на одного работника;
производительность труда, т.е. выработка продукции в единицу времени или на одного работника;
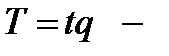 общие затраты времени на производство продукции.
общие затраты времени на производство продукции.
Каждый индекс включает данные за два периода: отчетный (текущий, сравниваемый) и базисный, который используется как база сравнения. Данные отчетного периода обозначаются подстрочным знаком 1 (например, 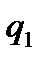 ), базисного – 0 (например,
), базисного – 0 (например, 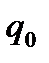 ).
).
По степени охвата элементов совокупности индексы делятся на индивидуальные и общие. Индивидуальные индексы обозначаются 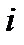 и снабжаются подстрочным знаком индексируемого показателя. Они характеризуют относительное изменение отдельного элемента совокупности и рассчитываются как отношение текущего уровня индексируемой величины к базисному уровню (т.е. по сути, являются коэффициентами или темпами роста).
и снабжаются подстрочным знаком индексируемого показателя. Они характеризуют относительное изменение отдельного элемента совокупности и рассчитываются как отношение текущего уровня индексируемой величины к базисному уровню (т.е. по сути, являются коэффициентами или темпами роста).
Так, индивидуальный индекс цен равен
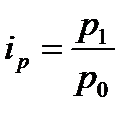 , (7.1)
, (7.1)
где 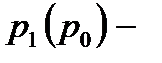 цена товара в текущем (базисном) периоде.
цена товара в текущем (базисном) периоде.
Индивидуальные индексы физического объёма
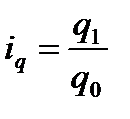 (7.2)
(7.2)
и товарооборота
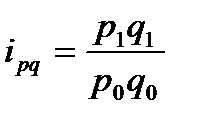 . (7.3)
. (7.3)
Индивидуальный индекс себестоимости характеризует изменение себестоимости отдельного вида продукции в текущем периоде по сравнению с базисным:
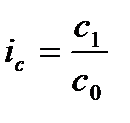 . (7.4)
. (7.4)
Индивидуальный индекс производительности труда определяется как отношение количества продукции, вырабатываемой в единицу времени или на одного работника в текущем периоде, к её базисному значению:
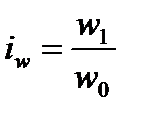 . (7.5)
. (7.5)
Индивидуальные индексы могут рассчитываться также и цепным методом. В этом случае цена товара в последующем году выражается в ценах предыдущего года.
Иногда индивидуальный индекс является средней других индексов. Например, индекс прожиточного минимума является средней взвешенной индексов цен покупаемых предметов; причем каждый индекс цен взвешивается по доле доходов, которая расходуется на этот предмет. Так, согласно таблице
| Наименование расходов | Доля | Индекс цен в 1987 г. по сравнению с 1986 г. | Доля *Индекс цен |
| Мясо | 5 *112 = 560 | ||
| Молочные продукты | 10 * 105 = 1050 | ||
| Овощи | 25 * 108 = 2700 | ||
| Суммарные расходы |
индекс прожиточного минимума равен 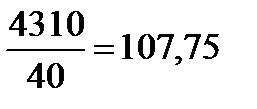 .
.
Если изучаемое явление неоднородно и сравнение уровней можно привести к сопоставимому виду только при помощи взвешивающих показателей, то в экономическом анализе этого явления используют общие (сводные) индексы, обозначаемые большой буквой 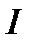 . Примером неоднородной совокупности является общая масса проданных товаров нескольких видов. Тогда сумма выручки записывается в виде “агрегата” (от латинского aggregatus - складываемый, суммируемый), т.е. суммы произведений взвешивающего показателя на объёмный; например:
. Примером неоднородной совокупности является общая масса проданных товаров нескольких видов. Тогда сумма выручки записывается в виде “агрегата” (от латинского aggregatus - складываемый, суммируемый), т.е. суммы произведений взвешивающего показателя на объёмный; например: 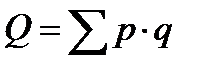 . Отношение агрегатов, построенных для разных условий, дает общий индекс показателя в агрегатной форме. Например, индекс общего объёма товарооборота в агрегатной форме имеет вид:
. Отношение агрегатов, построенных для разных условий, дает общий индекс показателя в агрегатной форме. Например, индекс общего объёма товарооборота в агрегатной форме имеет вид:
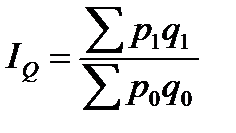 (7.6)
(7.6)
Здесь прирост общего объёма товарооборота объясняется изменением уровня цен и количества проданных товаров. Влияние на прирост товарооборота общего изменения цен выражается агрегатным индексом цен (в форме индекса Пааше):
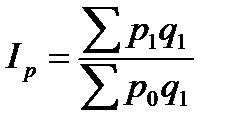 . (7.7)
. (7.7)
Влияние на прирост товарооборота изменения количества проданных товаров представляется агрегатным индексом физического объёма:
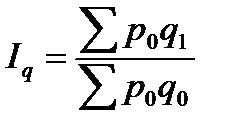 . (7.8)
. (7.8)
Все три вышеприведенных индекса 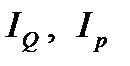 и
и 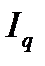 связаны между собой и представляют индексную мультипликативную модель динамики товарооборота, которая позволяет разложить индекс товарооборота по факторам:
связаны между собой и представляют индексную мультипликативную модель динамики товарооборота, которая позволяет разложить индекс товарооборота по факторам:
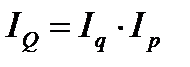 . (7.9)
. (7.9)
На основе этих индексов можно определить абсолютный прирост товарооборота 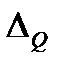 и разложить его по двум факторам. Из индекса товарооборота определяется общий абсолютный прирост – разница числителя и знаменателя:
и разложить его по двум факторам. Из индекса товарооборота определяется общий абсолютный прирост – разница числителя и знаменателя:
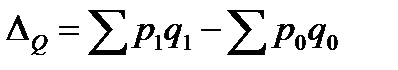 . (7.10)
. (7.10)
Абсолютный прирост товарооборота за счет изменения цен и за счет изменения физической массы определяется соответственно по формулам:
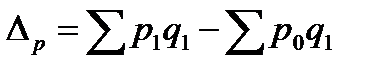 , (7.11)
, (7.11)
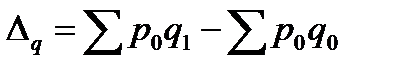 . (7.12)
. (7.12)
Сумма этих частных абсолютных приростов образует общий абсолютный прирост товарооборота, представленный индексной аддитивной моделью:
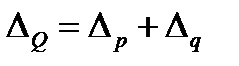 . (7.13)
. (7.13)
Пример 7.1.Имеются данные за два периода в ценах и объемах реализации трех видов товаров по одному из торговых предприятий:
Рассчитать: 1) индивидуальные индексы: цен, физического объема и товарооборота; 2) общие индексы: цен, физического объема и товарооборота; 3) абсолютный прирост товарооборота. Решение: 1) индивидуальные индексы: цен (7.1): физического объема (7.2): товарооборота (7.3): 2) общие индексы: цен (7.7): физического объема (7.8): товарооборота (7.6): Проверим (7.9): 3) абсолютный прирост товарооборота (7.10): за счет цен (7.11) за счет объема (7.12) |
Особенности использования агрегатного индекса цен 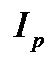 . Он используется в двух формах: индексов Пааше и Ласпейреса.
. Он используется в двух формах: индексов Пааше и Ласпейреса.
В индексе Пааше в качестве соизмерителя используется объем продукции соответствующего вида в текущем периоде 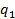 . Индекс Пааше рассчитывается по формуле (7.7), где
. Индекс Пааше рассчитывается по формуле (7.7), где 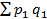 - стоимость всей продукции в текущем периоде;
- стоимость всей продукции в текущем периоде; 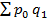 - условная стоимость продукции текущего периода по сопоставимым ценам базисного периода.
- условная стоимость продукции текущего периода по сопоставимым ценам базисного периода.
Индекс цен Пааше характеризует влияние изменения цен на стоимость товаров, которые реализованы в текущем периоде. Этот индекс используют при изучении отчетных данных.
Например, если 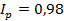 (или 98%), то это означает, что уровень цен на товары, которые реализованы в текущем периоде, в среднем уменьшился в 0,98 раза (или на 2%) по сравнению с базисным периодом. В случае
(или 98%), то это означает, что уровень цен на товары, которые реализованы в текущем периоде, в среднем уменьшился в 0,98 раза (или на 2%) по сравнению с базисным периодом. В случае 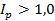 (или 100%) говорят об увеличении цен в текущем периоде по сравнению с базисным периодом.
(или 100%) говорят об увеличении цен в текущем периоде по сравнению с базисным периодом.
Разность (7.11) соответствует абсолютной экономии (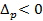 ) или абсолютному перерасходу (
) или абсолютному перерасходу (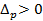 ) денежных средств покупателей в результате изменения цен на эти товары.
) денежных средств покупателей в результате изменения цен на эти товары.
В индексе Ласпейреса в качестве соизмерителя используется объем продукции соответствующего вида в базисном периоде 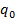 :
:
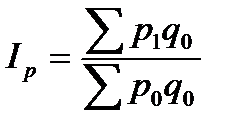 , (7.14)
, (7.14)
где 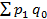 - стоимость всей продукции в базисном периоде по ценам текущего периода;
- стоимость всей продукции в базисном периоде по ценам текущего периода;
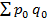 - стоимость продукции в базисном периоде.
- стоимость продукции в базисном периоде.
Индекс Ласпейреса показывает влияние изменения цен на стоимость товаров, которые реализованы в базисном периоде. Его используют при прогнозировании объема товарооборота в связи с возможным изменением цен на товары в будущем периоде.
Агрегатный индекс себестоимости продукции имеет вид:
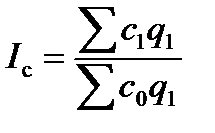 , (7.15)
, (7.15)
где 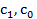 – себестоимость единицы продукции определенного вида соответственно в текущем и базисном периодах;
– себестоимость единицы продукции определенного вида соответственно в текущем и базисном периодах;
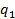 - объем продукции текущего периода;
- объем продукции текущего периода;
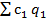 – расходы на производство продукции в текущем периоде;
– расходы на производство продукции в текущем периоде;
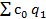 - условные расходы на производство той же продукции, если себестоимость единицы продукции была на уровне базисного периода.
- условные расходы на производство той же продукции, если себестоимость единицы продукции была на уровне базисного периода.
Агрегатный индекс трудоемкости имеет вид:
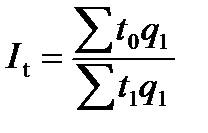 , (7.16)
, (7.16)
где 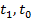 – затраты рабочего времени на единицу продукции (трудоемкость) соответственно в текущем и базисном периодах;
– затраты рабочего времени на единицу продукции (трудоемкость) соответственно в текущем и базисном периодах;
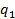 - объем продукции в текущем периоде;
- объем продукции в текущем периоде;
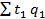 – фактические затраты рабочего времени на всю продукцию в текущем периоде;
– фактические затраты рабочего времени на всю продукцию в текущем периоде;
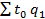 - условные затраты рабочего времени (трудоемкость) на всю продукцию в базисном периоде.
- условные затраты рабочего времени (трудоемкость) на всю продукцию в базисном периоде.
Аналогично (7.9) агрегатный индекс общей себестоимости продукции 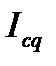 можно представить в виде:
можно представить в виде:
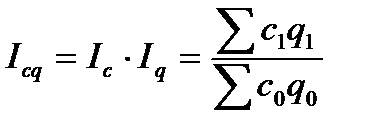 , (7.17)
, (7.17)
который показывает сопоставление расходов на производство продукции в текущем и базисном периодах и выражается в коэффициентах или процентах.
Агрегатный индекс общих расходов рабочего времени 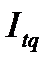 :
:
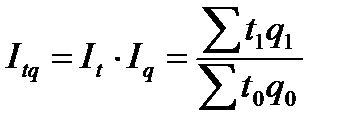 , (7.18)
, (7.18)
Эта величина дает сравнение расходов рабочего времени на производство продукции разных видов в текущем и базисном периодах.
 2015-05-13
2015-05-13 2254
2254
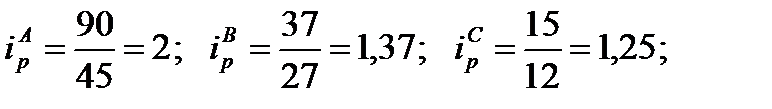
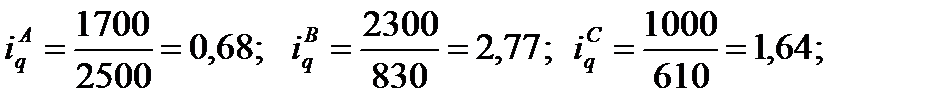
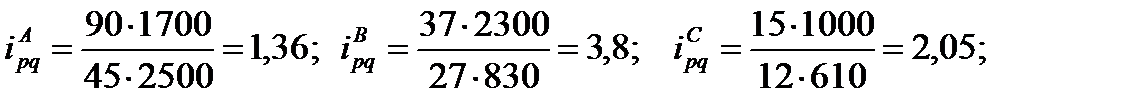
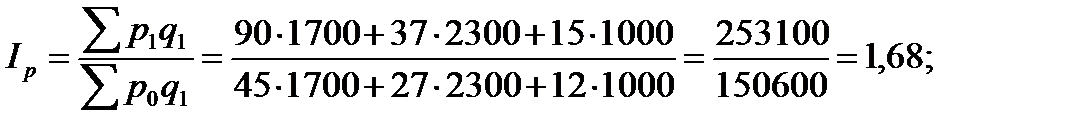
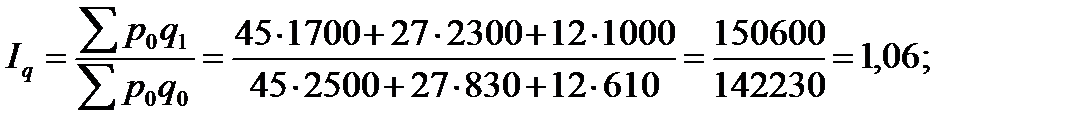
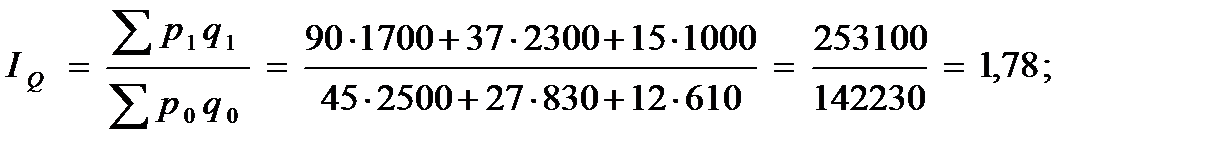
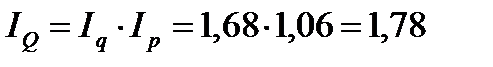 .
.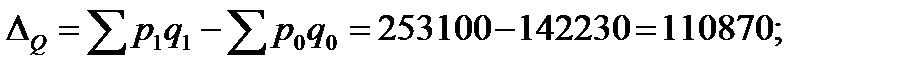
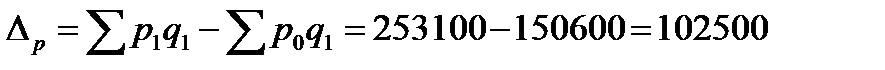 или 92,45 %;
или 92,45 %;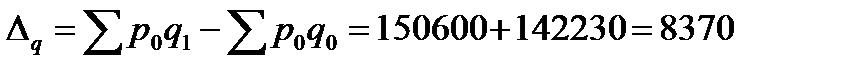 или 7,55 %.
или 7,55 %.






