Рассмотрим случай, когда эксперты ранжируют объекты строго, т.е. указывают номер места, которое занимает данный объект по важности. Обозначим:
 число объектов;
число объектов;
 число экспертов;
число экспертов;
 ранг, присвоенный
ранг, присвоенный  м экспертом
м экспертом  у объекту.
у объекту.
Результаты сводят в таблицу:
 .
.
Затем находят суммы рангов по столбцам:  где
где  .
.
Объекты ранжируют в соответствии с суммами рангов: объект  предпочтительнее объекта
предпочтительнее объекта  , если
, если  ; объекты
; объекты  и
и  эквивалентны, если
эквивалентны, если  .
.
Далее необходимо оценить согласованность экспертов.
Пусть все эксперты совершенно согласованы, т.е. дают одинаковые ранги объектам. В этом случае суммы рангов по столбцам будут:  , т.е. в одном столбце все единицы, в другом только двойки и т.д.
, т.е. в одном столбце все единицы, в другом только двойки и т.д.
Сумма чисел в одной строке:  .
.
Общая сумма рангов во всей матрице:  .
.
Если эксперты полностью рассогласованы, то ранги равны:
 . (8.1)
. (8.1)
Разброс мнений экспертов будем характеризовать следующим образом. Найдем отклонение суммы рангов в таблице от  :
:  . Так как разности будут разного знака, то суммируют квадраты разностей
. Так как разности будут разного знака, то суммируют квадраты разностей
 . (8.2)
. (8.2)
Если эксперты полностью согласованы, то сумма  максимальна. Если эксперты полностью рассогласованы, то
максимальна. Если эксперты полностью рассогласованы, то  . Обозначим
. Обозначим  наибольшее значение
наибольшее значение  , соответствующее случаю полной согласованности экспертов.
, соответствующее случаю полной согласованности экспертов.
Для оценки согласованности экспертов вводится коэффициент конкордации (согласованности):
 . (8.3)
. (8.3)
Если  , то полное отсутствие согласованности. Если
, то полное отсутствие согласованности. Если  , то полная согласованность.
, то полная согласованность.
Найдем 
первый член суммы – 
второй – 
и т.д. 
.....................................................
 .
.
После суммирования получим:  . Окончательно получаем:
. Окончательно получаем:
 . (8.4)
. (8.4)
Если эксперты неквалифицированны и друг от друга не зависят, то тогда  можно рассматривать как случайную величину
можно рассматривать как случайную величину  , для которой известно распределение.
, для которой известно распределение.
Можно найти вероятность того, что значение коэффициента конкордации получено случайно, т.е. вероятность
 .
.
Значение  можно рассматривать, как доверительную вероятность. Если она достаточно мала, а
можно рассматривать, как доверительную вероятность. Если она достаточно мала, а  достаточно велико, то предположение об отсутствии согласованности отклоняется. Обычно согласованность считают удовлетворительной, если
достаточно велико, то предположение об отсутствии согласованности отклоняется. Обычно согласованность считают удовлетворительной, если  и
и  и хорошей, если
и хорошей, если  и
и  .
.
Для малых значений  и
и  составлены специальные таблицы распределения
составлены специальные таблицы распределения  , например, таблица значений коэффициента конкордации, для которых вероятность ошибки при принятии гипотезы о согласованности мнений экспертов не превосходит 0,05.
, например, таблица значений коэффициента конкордации, для которых вероятность ошибки при принятии гипотезы о согласованности мнений экспертов не превосходит 0,05.
 \ \  | |||||
| - | - | 0,71 | 0,66 | 0,65 | |
| - | 0,625 | 0,55 | 0,51 | 0,505 | |
| - | 0,504 | 0,448 | 0,416 | 0,411 | |
| - | 0,422 | 0,378 | 0,351 | 0,347 | |
| 0,375 | 0,319 | 0,288 | 0,267 | 0,264 | |
| 0,3 | 0,256 | 0,231 | 0,215 | 0,213 |
При  можно считать, что величина
можно считать, что величина  имеет распределение близкое к распределению
имеет распределение близкое к распределению  с
с  степенями свободы.
степенями свободы.
Пример 8.1.Пять экспертов ранжировали восемь объектов  . Результаты приведены в таблице. . Результаты приведены в таблице.
Находим ранг объектов при полном рассогласовании экспертов (8.1): Сумма отклонений (8.2): Коэффициент конкордации (8.4): По таблицам (Приложение) находим Вероятность слишком велика. Для сближения оценок экспертов нужно провести дополнительный тур оценивания, либо исключить второго эксперта, как слишком “оригинального”. После исключения второго эксперта получаем новую таблицу
Производим все вычисления в таком же порядке:
По таблицам (Приложение) находим |
 2015-05-13
2015-05-13 709
709

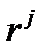

 .
.
 .
.  .
. .
.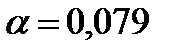 .
. :
: ;
;
 ;
; ;
; . Согласованность экспертов значительно лучше.
. Согласованность экспертов значительно лучше.






