В 1905 году А. Эйнштейн объяснил фотоэффект на основании квантовых представлений. Согласно Эйнштейну, свет не только испускается квантами в соответствии с гипотезой Планка, но распространяется в пространстве и поглощается веществом отдельными порциями - квантами с энергией E0 = hv. Кванты электромагнитного излучения называются фотонами.
Уравнение Эйнштейна (закон сохранения энергии для внешнего фотоэффекта):
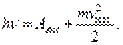
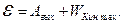
Энергия падающего фотона hv расходуется на вырывание электрона из металла, то есть на работу выхода Авых, и на сообщение вылетевшему фотоэлектрону кинетической энергии 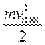 .
.
Наименьшая энергия, которую необходимо сообщить электрону для того, чтобы удалить его из твердого тела в вакуум называется работой выхода.
Так как энергия Ферм к ЕF зависит от температуры и ЕF, также изменяется при изменении температуры, то, следовательно, Авых зависит от температуры.
Кроме того, работа выхода очень чувствительна к чистоте поверхности. Нанеся на поверхность пленку (Са, Sг, Ва) на W Авых уменьшается с 4,5 эВ для чистого W до 1,5 ÷ 2 эВ для примесного W.
Уравнение Эйнштейна позволяет объяснить вcе три закона внешнего фотоэффекта,
1-й закон: каждый квант поглощается только одним электроном. Поэтому число вырванных фотоэлектронов должно быть пропорционально интенсивности (Ф) света
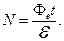
2-й закон: Vmax ~ ν и т.к. Авых не зависит от Ф, то и Vmax не зависит от Ф
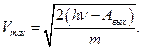
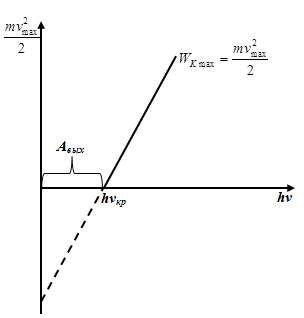
3-й закон: При уменьшении ν уменьшается Vmax и при ν = ν0 Vmax = 0, следовательно, hν0 = Авых, следовательно, 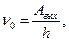 т.е. существует минимальная частота, начиная с которой возможен внешний фотоэффект.
т.е. существует минимальная частота, начиная с которой возможен внешний фотоэффект.
Фотон - элементарная частица, которая всегда (в любой среде!) движется со скоростью света с и имеет массу покоя, равную нулю. Следовательно, масса фотона отличается от массы таких элементарных частиц, как электрон, протон и нейтрон, которые обладают отличной от нуля массой покоя и могут находиться в состоянии покоя.
Импульс фотона рg получим, если в общей формуле теории относительности положим массу покоя фотона m0g = 0:
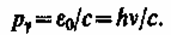
Рассеяние излучения на свободных электронах
Рассмотрим движение электрона в плоской электромагнитной волне: 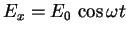 , распространяющейся вдоль оси
, распространяющейся вдоль оси 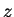 . Уравнение движения электрона:
. Уравнение движения электрона:
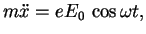
и энергия, излучаемая таким электроном,
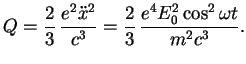
Своих источников энергии у электрона нет. Фактически он переизлучает (рассеивает) энергию падающей электромагнитной волны в других направлениях, так что
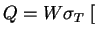 эрг
эрг 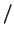 с
с 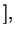
где 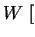 эрг
эрг 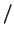 см
см 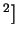 -- поток падающей энергии:
-- поток падающей энергии:
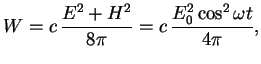
и сечение рассеяния
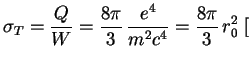 см
см 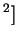
знаменитая формула Томсона. Величина
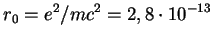 см
см 
называется классическим радиусом электрона.
При преобладающей роли электронного рассеяния (процессы поглощения излучения несущественны) изменение интенсивности 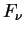 в монохроматическом пучке фотонов, очевидно, равно
в монохроматическом пучке фотонов, очевидно, равно
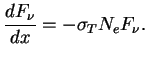
Можно ввести коэффициент ``поглощения'' при томсоновском рассеянии (хотя реально поглощения энергии и нет):
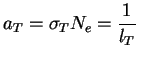 см
см 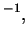
где длина пробега
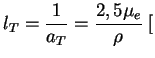 см
см 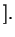
Интегрируя уравнение для 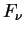 , получаем
, получаем
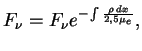
т.е. 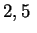 г/см
г/см 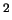 водородной плазмы (
водородной плазмы (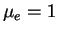 ) уменьшают
) уменьшают 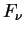 в
в 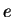 раз за счет электронного рассеяния.
раз за счет электронного рассеяния.
Теория эффекта Комптона [править | править исходный текст]
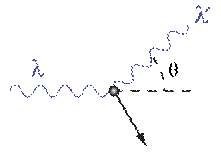

Иллюстрация к эффекту Комптона. Излучение с длиной волны 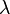 направлено слева направо. После взаимодействия с электроном оно меняет длину волны на
направлено слева направо. После взаимодействия с электроном оно меняет длину волны на 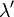 , а направление на угол
, а направление на угол 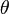 относительно первоначального направления. Стрелкой указано направление движения электрона, с которым провзаимодействовал фотон.
относительно первоначального направления. Стрелкой указано направление движения электрона, с которым провзаимодействовал фотон.
При рассеянии фотона на покоящемся электроне частоты фотона 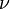 и
и 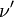 (до и после рассеяния соответственно) связаны соотношением:
(до и после рассеяния соответственно) связаны соотношением:
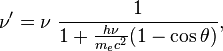
где 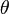 — угол рассеяния (угол между направлениями распространения фотона до и после рассеяния).
— угол рассеяния (угол между направлениями распространения фотона до и после рассеяния).
Перейдя к длинам волн:
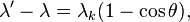
где 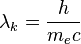 — комптоновская длина волны электрона, равная
— комптоновская длина волны электрона, равная 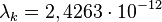 м.
м.
Уменьшение энергии фотона в результате комптоновского рассеяния называется комптоновским сдвигом. Объяснение эффекта Комптона в рамках классической электродинамики невозможно, так как рассеяние электромагнитной волны на заряде (томсоновское рассеяние) не меняет её частоты.
Эффект Комптона является одним из доказательств справедливости корпускулярно-волнового дуализмамикрочастиц и подтверждает существование фотонов.
Закон сохранения энергии в случае эффекта Комптона можно записать следующим образом[1]:
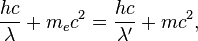
где 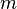 — релятивистская масса электрона, выражаемая через его скорость
— релятивистская масса электрона, выражаемая через его скорость 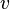 следующей формулой:
следующей формулой:
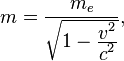
Сечение эффекта Комптона описывается формулой Клейна-Нишины.
 2015-05-13
2015-05-13 1220
1220








