2015-05-13
968
Найдем взаимосвязь между напряженностью электростатического поля — силовой характеристикой поля, и потенциалом — энергетической характеристикой поля.
Работа по перемещению единичного точечного положительного заряда из одной точки поля в другую вдоль оси x
dA = Exdx.
Та же работа равна
dA = - dφ
Приравняв оба выражения, можем записать
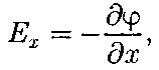
Где символ частной производной подчеркивает, что дифференцирование производится только по x. Повторяя рассуждения для осей y и z получим:
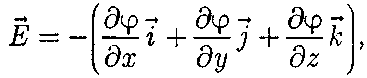
Или
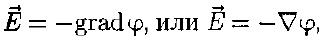
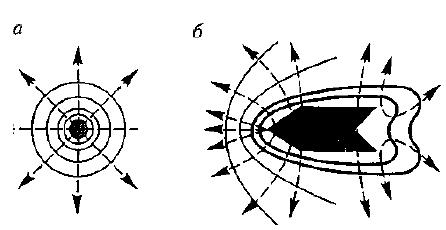
Для графического изображения распределения потенциала электростатического поля пользуются эквипотенциальными поверхностями — поверхностями, во всех точках которых потенциал φ имеет одно и то же значение.
Линии напряженности всегда нормальны к эквипотенциальным поверхностям.
Однако их обычно проводят так, чтобы разности потенциалов между любыми двумя соседними эквипотенциальными поверхностями были одинаковы. Тогда густота эквипотенциальных поверхностей наглядно характеризует напряженность поля в разных точках.
Вычисление разности потенциалов по напряженности поля
