Таким образом, точное решение можно получить только в результате бесконечного процесса

На практике итерационный процесс должен быть ограничен конечным числом шагов (итераций) n. Количество итераций зависит от требуемой точности нахождения корня.

Для прекращения итерационного процесса применяются различные критерии, зависящие от вида функции y=f(x) в окрестности корня.

1. Если функция достаточно «пологая» в окрестности корня, то итерационный процесс продолжается до тех пор, пока две соседние итерации не станут достаточно близкими, т.е. пока не выполнится условие

|x_n-1 - x_n|< e (1.4)

1. Если функция у=f(x) «круто» меняет свои значения в окрестности корня, то целесообразно использовать условие

|f(x_n)|<e (1.5)

Если хоты бы одно из условие (1.4) или (1.5) выполняется, то в качестве приближенного решения уравнения (1.1) с точностью e принимается n-я итерация, т.е..

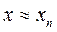Если ни одно из этих условий не выполняется, то итерационный процесс (1.3) необходимо продолжить.

Рассмотрим несколько итерационных методов решения нелинейных уравнений.

Использование приближенных методов для решения уравнения f (x) = 0 возможно лишь в том случае, когда функция f(x) удовлетворяет следующим условиям Теоремы1:

1. функция f(x) непрерывна на отрезке [a, b];

2. значения функции f(x) на концах отрезка имеют разные знаки (f(a) f(b) < 0);