2015-05-13
354
· определить количество действительных корней и
· локализовать их, т.е. выделить отрезок, на котором уравнение (1.2) имеет единственный корень. Иначе говоря, выделить отрезок, на котором функция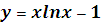 
непрерывна, принимает разные знаки на концах отрезка, т.е. f(a) f(b)<0 и монотонна для [a, b], т.е. производная f’(x) сохраняет знак.
Для этого протабулируем функцию 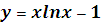для xÎ ОДЗ и построим ее график.
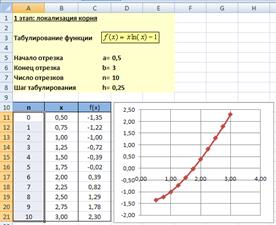
| Разобьем это задание на несколько более мелких заданий, выполняя их последовательно друг за другом. Введите в ячейки: 1. А5 текст начало отрезка, А6 текст конец отрезка, А7 текст число отрезков, А8 текст шаг табулирования 2. С5: a=, D5 = 0.5, С6: b=, D6 = 3, С7: n=, D7 = 10, С8: h=, D8 = (D6-D5)/D7 3. Подготовьте таблицу из 3-х столбцов (n,Х и f(x)), Числовые значения для Х заполняем следующим образом: · в ячейку B11 =D5, · в ячейку B12 =B11+$D$8, · выделите ячейку B12, установите курсор в правый нижний угол (появится черный крестик) и тяните её до конца таблицы (пока Х не станет равным 3) Числовые значения для f(x): · в ячейку C11 =B11*ln(B11)-1, · выделите ячейку C11 и тяните ее до конца таблицы График функции постройте с помощьюМастера диаграмм |
Поскольку производная нашей функции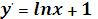 
существует и не изменяет знак для xÎ [0.5, 3], т.е. выполняются условия Теоремы1, то анализ таблицы и графика функции показывает, что на отрезке [0.5, 3] уравнение имеет единственный корень.
|
|
|
