Пусть уравнение f (x) = 0, на отрезке [a,b] удовлетворяет условиям теоремы 1, т.е. имеет единственный корень, и 2-ая производная f’’(x) имеет постоянный знак.
Геометрически метод Ньютона заключается в замене небольшого участка дуги кривой y=f(x) касательной, проведенной в некоторой точке к этой кривой.
| Для решения нелинейного уравнения по методу касательных справедлива Теорема 2. |
Пусть функция y = f(x) на отрезке [a,b] удовлетворяет условиям теоремы 1, т.е. уравнение (1.1) имеет на этом отрезке единственный корень. Если функция y=f(x) имеет 2-ую производную, сохраняющую знак на этом отрезке, то исходя из начального приближения х0 , удовлетворяющего условию: f(x0) f ’’ (x0)>0, (1.6) корень уравнения (1) можно вычислить с точностью e по формуле 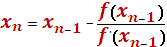 (1.7) (1.7) |
Рассмотрим случай, когда f ’’(x)>0 для xÎ [a, b], f(a)<0 и f(b)>0.
Напомним, что знак второй производной функции легко определить из графика самой функции.
Если график функции выпуклый внизу, то вторая производная функции больше нуля (f ’’ (x)>0).
Если график функции выпуклый кверху, то вторая производная меньше нуля (f ’’ (x)<0).
 2015-05-13
2015-05-13 711
711








