Пусть уравнение f(x) = 0, на отрезке [a,b] удовлетворяет условиям теоремы 1, т.е. имеет единственный корень, и производные f’(x) и f’’(x) непрерывны и имеют постоянные знаки.
С геометрической точки зрения метод хорд эквивалентен замене кривой y = f(x) хордой, проходящей через точки A[a, f(a)] и B[b, f(b)].
| Для решения нелинейного уравнения по методу хорд справедлива Теорема 3. |
Пусть функция y = f(x) на отрезке [a,b] удовлетворяет условиям теоремы 1, т.е. уравнение (2.1) имеет на этом отрезке единственный корень.
Исходя из начального приближения x0, удовлетворяющего условию
f(x0) f ’’ (x0)<0, (1.8)
корень x* уравнения (2.1) с заданной точностью ε вычисляется по формуле
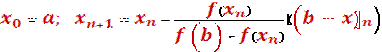 (1.9)
или (1.9)
или
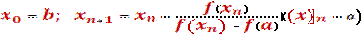 (1.10) (1.10)
|
Напомним, что знак второй производной функции легко определить из графика самой функции.
Возможны несколько вариантов расположения графика функции на отрезке [a,b].
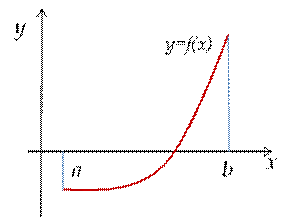
| Если график функции выпуклый внизу, то вторая производная функции больше нуля f ’’ (x0)>0 | |
| 
|
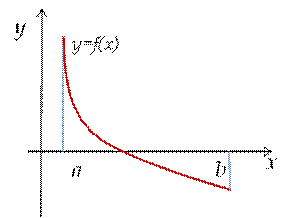
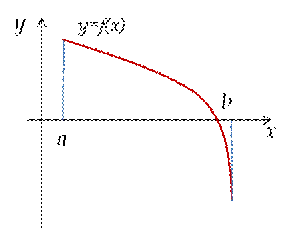
| Если график функции выпуклый кверху, то вторая производная меньше нуля f ’’ (x0)<0 | |
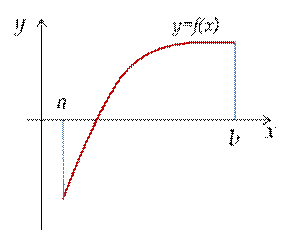
| 
|
Рассмотрим 1-ый случай, когда f ’’ (x)>0 для xÎ [a,b], f(а)<0, f(b)>0 ( см. рисунок ниже)
 2015-05-13
2015-05-13 633
633








