1. За начальное приближение берем 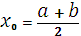 , т.е. делим отрезок [a, b] пополам. 2.Если значение функции в этой точке равно 0, т.е , т.е. делим отрезок [a, b] пополам. 2.Если значение функции в этой точке равно 0, т.е 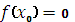 , то x0 является корнем уравнения 3.Если , то x0 является корнем уравнения 3.Если 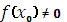 , то из двух отрезков [a, x] и [x, b] выбираем тот, на концах которого функция f(x) имеет разные знаки (из рисунка видно, что f(x) > 0, f(a)< 0, f(b) > 0, значит выбираем отрезок [a, x]. Точку b переносимв x0. 4.Далее итерационный процесс продолжается путем деления нового отрезка пополам, т.е. новый «суженный» отрезок [a1, b1] снова делим пополам и проводим тот же анализ. т.е. повторяем п. 2. 5.Процесс деления отрезка пополам прекращается, когда , то из двух отрезков [a, x] и [x, b] выбираем тот, на концах которого функция f(x) имеет разные знаки (из рисунка видно, что f(x) > 0, f(a)< 0, f(b) > 0, значит выбираем отрезок [a, x]. Точку b переносимв x0. 4.Далее итерационный процесс продолжается путем деления нового отрезка пополам, т.е. новый «суженный» отрезок [a1, b1] снова делим пополам и проводим тот же анализ. т.е. повторяем п. 2. 5.Процесс деления отрезка пополам прекращается, когда 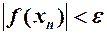 | 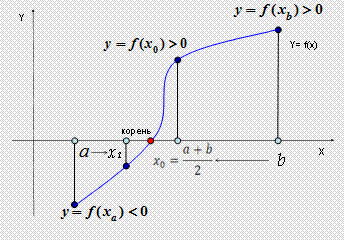 Если условие выполняется, то полученная в результате вычислений последняя точка хn является приближённым значением корня уравнения, найденным с погрешностью e. Если условие не выполняется, то итерационный процесс необходимо продолжить. Если условие выполняется, то полученная в результате вычислений последняя точка хn является приближённым значением корня уравнения, найденным с погрешностью e. Если условие не выполняется, то итерационный процесс необходимо продолжить. |
2 этап. Уточнение корня уравнения. Реализация метода половинного деления (дитохомии)
Задание 2.4. Уточнение корня уравнения (1.2) методом половинного деления.
| Последовательность действий. 1.Подготовьте таблицу, как показано на рисунке 2. Введите в ячейки: A5 текст Начало отрезка a=, E5 = 0.5, A6 текст Конец отрезка b=, E6 = 3.0, A7 текст Начальное приближение x0=, E7 = (E5+E6)/2, A8 текст Точность вычисления e=, E8 = 0.01 3.Используя автозаполнение введите номер итерации nв столбце А. 4.Заполните 1-строку таблицы: Введите в ячейки: В13 = Е5 (значение a) C13 = Е6 (значение b) D13= B13*ln(B13)-1 (формулу для f(а)) E13= C13*ln(C13)-1 (формулу для f(b)) F13 = (B13+C13)/2 (формулу для вычисления середины отрезка), G13= F13*ln(F13)-1 (формулу для f(x)) H13 = ABS(G13)(модуль значения функции) 5. B14 =ЕСЛИ(D13*G13<0; B13; F13); (формулу для формирования левого конца отрезка, используя функцию ЕСЛИ), C14 =ЕСЛИ(D13*G13<0; F13; C13), (формулу для формирования правого конца отрезка, используя функцию ЕСЛИ). 6.Выделите ячейки D13-H13 и скопируйте на строку ниже, т.е. соответственно в D14-H14 и вы получите f(a), f(b), x, f(x) и |f(x)| в точке первого приближения х1. 7.Выделите блок ячеек В14-H14 и скопируйте их вниз до конца таблицы. 8.Итерационный процесс следует продолжить до тех пор, пока не выполнится условие |f(xn)|< e Ячейки H19-H21 тонированы серым цветом с использованием Условного форматирования(см. выше – в методе касательных) | 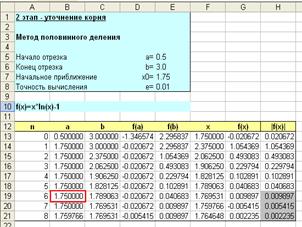 За приближенное решение уравнения по методу половинного деления с заданной точностью e=0.01 принимается 6-я итерация, т.е. x* »1,7500. За приближенное решение уравнения по методу половинного деления с заданной точностью e=0.01 принимается 6-я итерация, т.е. x* »1,7500. |
3. Чтобы сделать наглядным окончание итерационного процесса воспользуйтесь Условным форматированием (установки см. в методе касательных)
 2015-05-13
2015-05-13 1511
1511
