1. Выберем начальное приближение. Начальное приближение x0 выбирается,исходя из условия f(x0) f ’’(x0) <0. Данное условие выполняется в т. x0 = a. 2.Проведем хорду к кривой y = f(x) через точки A[a, f(a)] и B[b, f(b)]. 3.В качестве 1-го приближения корня х1 возьмем абсциссу точки пересечения этой хорды с осью ОХ. 4.Через точки C[x1, f(x1)] и B[b, f(b)] снова проведем хорду, абсцисса точки пересечения которой с осью ОХ даст нам второе приближение корня х2 и т.д. 5.Продолжим процесс, в результате получим итерационную последовательность x0, x1, x2,……xn; 6. Ф ормула для вычисления n-ого приближения 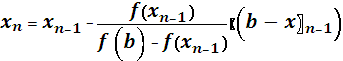 7.Итерационный процесс продолжается (или построение хорд продолжается) до тех пор, пока две соседние итерации не станут достаточно близкими, т.е. пока не выполнится условие 7.Итерационный процесс продолжается (или построение хорд продолжается) до тех пор, пока две соседние итерации не станут достаточно близкими, т.е. пока не выполнится условие 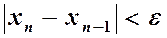 Или Или 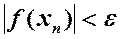 | 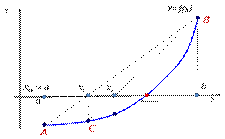 Если хоты бы одно из условие (1.4) или (1.5) выполняется, то в качестве приближенного решения уравнения (1.1) с точностью e принимается n-я итерация, т.е. Если хоты бы одно из условие (1.4) или (1.5) выполняется, то в качестве приближенного решения уравнения (1.1) с точностью e принимается n-я итерация, т.е. 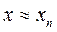 Если ни одно из условий не выполняется, то итерационный процесс необходимо продолжить. Если ни одно из условий не выполняется, то итерационный процесс необходимо продолжить. |
2 этап. Уточнение корня уравнения. Реализация метода хорд
Задание 2.3. Уточнение корня уравнения (2.2) методом хорд проводим на основании теоремы 3.
4. Найдем начальное приближение x0, исходя из условия f(x0) f ’’ (x0)<0.
Для функции  вторая призводная f ’’ (x)=1/х положительна на всем отрезке [0.5, 3] (знак второй производной функции можно определить и по графику функции), f(0.5)<0, f(3.0)>0, следовательно x0=a=0.5 ( Из рассмотренных выше случаях у нас 1 вариант)
вторая призводная f ’’ (x)=1/х положительна на всем отрезке [0.5, 3] (знак второй производной функции можно определить и по графику функции), f(0.5)<0, f(3.0)>0, следовательно x0=a=0.5 ( Из рассмотренных выше случаях у нас 1 вариант)
2. Корень уравнения x* с заданной точностью ε вычисляется по формуле (1.9)
| Последовательность действий. 1.Подготовьте таблицу, как показано на рисунке 2. Введите в ячейки: A5 текст Начало отрезка a=, E5 = 0.5, A6 текст Конец отрезка b=, E6 = 3.0, A7 текст Начальное приближение x0=, E7 = E5, A8 текст Точность вычисления e=, E8 = 0.01 3.Используя автозаполнение введите номер итерации nв столбце А. 4. Введите в ячейки: В13 =Е7(т.е. значение x0) C13 =B13*ln(B13)-1(формулу для вычисления значения функции), D13 =$E$6-B13 (т.е.b-x), E13 =$D$10-C13, (т.е. f(b)-f(x)), F13 =ABS(C13), (т.е |f(x)|) 5. B14 =B13-C13/E13*D13 (формулу для вычисления 1-го приближения). 6.Выделите ячейки C13, D13, E13, F13 и скопируйте на строку ниже, т.е. соответственно в C14, D14, E14, F14 и вы получите f(x), b-x, f(b)-f(x), |f(x)| в точке первого приближения х1. 7.Выделите блок ячеек В14-F14 и скопируйте их вниз до конца таблицы. 8.Итерационный процесс следует продолжить до тех пор, пока не выполнится условие |f(xn)|< e Ячейки F17-E18 тонированы серым цветом с использованием Условного форматирования(см. выше – в методе касательных) | 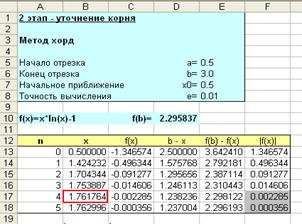 За приближенное решение уравнения по методу хорд с заданной точностью e=0.01 принимается 4-я итерация, т.е. x* »1,761764. За приближенное решение уравнения по методу хорд с заданной точностью e=0.01 принимается 4-я итерация, т.е. x* »1,761764. |
Чтобы сделать наглядным окончание итерационного процесса воспользуйтесь Условным форматированием (установки см. в методе касательных)
 2015-05-13
2015-05-13 2633
2633








