Замена переменных в кратном интеграле. Полярные и сферические координаты

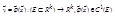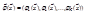
Пусть функция , , 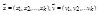dx=dx₁dx₂…dx_k, dy=dy₁dy₂…dy_k 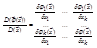- якобиан преобразования 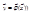, отличный от нуля почти всюду в E.

Пусть 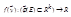интегрируема по Риману на этом мн-ве E^*=φ(E), тогда 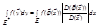. Теорема принимается без доказательства.

Сформулируем теорему для к=2 и к=3

R²: 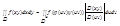; x=φ(uv),y=ψ(uv), D→D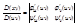^* φ,ψcC¹(E)

R³: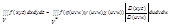

x=φ(uvw)

y=ψ(uvw) V→V^* φψχ c C¹_V*

z=χ(uvw)

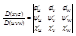
Полярные координаты в двойном интеграле.

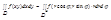
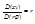
x=r∙cosφ

y=r∙sinφ

Сферические координаты в тройном интеграле

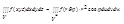
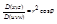
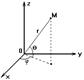
x=r∙cosθ∙cosφ 0≤φ≤2π

y=r∙cosθ∙sinφ -π/2≤θ≤π/2

z=r∙sinθ