1. Ecли f(x): R k -> R интегр-ма на допустимом мн-ве E из R k и равна нулю почти всюду на этом мн-ве, то 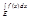 =0 2.(Линейность) Если E из R k допустимое и f(x) и g(x) интегрир по Р. на E то для любых действ α и β справедливо: αf(x)+βg(x) – тоже интегрир. на E и имеет место рав-во:
=0 2.(Линейность) Если E из R k допустимое и f(x) и g(x) интегрир по Р. на E то для любых действ α и β справедливо: αf(x)+βg(x) – тоже интегрир. на E и имеет место рав-во: 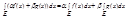 3. Если E1 и E2 из R k – два допуст-х мн-ва и f(x) – интегрир. по Р. на E1
3. Если E1 и E2 из R k – два допуст-х мн-ва и f(x) – интегрир. по Р. на E1 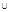 E2 и m(E1
E2 и m(E1 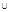 E2)=0 то
E2)=0 то 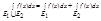 . Д-во: 1) J
. Д-во: 1) J 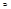 E, Р – разб-е J на J1...Jn Тогда всегда можно выбрать ξi
E, Р – разб-е J на J1...Jn Тогда всегда можно выбрать ξi  Ji так что σ(P,fχE) =
Ji так что σ(P,fχE) = 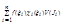 =0; А т.к. по условию существует limσ независимо от выбора ξi,получаем что
=0; А т.к. по условию существует limσ независимо от выбора ξi,получаем что 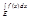 =
= 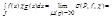 0. 2) Пусть J – любой промежуток, содержащий E. Тогда используя определение интегр. по промеж. имеем:
0. 2) Пусть J – любой промежуток, содержащий E. Тогда используя определение интегр. по промеж. имеем: 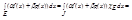
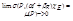
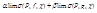 =
= 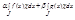 =
= 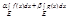 3) Если f(x) интегр. на E1
3) Если f(x) интегр. на E1 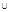 E2 то в силу критерия Лебега эта ф-ция имеет мн-во точек разрыва меры 0 на мн-ве E1
E2 то в силу критерия Лебега эта ф-ция имеет мн-во точек разрыва меры 0 на мн-ве E1 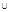 E2 и следовательно имеет мн-во точек разырыва меры 0 на любом подмн-ве, а значит f(x) интегрир. по Р. на любом подмн-ве т.е и на E1 и на E2. Т.к.
E2 и следовательно имеет мн-во точек разырыва меры 0 на любом подмн-ве, а значит f(x) интегрир. по Р. на любом подмн-ве т.е и на E1 и на E2. Т.к. 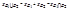 имеем:
имеем: 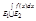 =
= 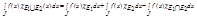 = {т.к.
= {т.к. 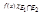 равна нулю почти всюду на E1
равна нулю почти всюду на E1 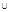 E2} =
E2} = 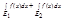 .
.
Теорема о свойствах интеграла Римана, выражаемых равенствами
|
|

Сейчас читают про:
 2015-05-13
2015-05-13 319
319







