2015-05-13
414
Ec R k – допустим. мн-во.
1) Если f(x) интегрир на Е, то |f(x)| также интегрир на Е и имеем место нер-во |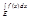 
| ≤ 
2) Если f(x) интегрир на Е и f(x)≥0 для всех x из Е то 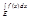≥0. 3) Если Если f(x) и g(x) интегрир на Е и для всех x из Е вып-ся: f(x)≤g(x) то ≤ 
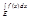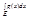. Д-во: Из того, что f(x) интегрир на Е согласно критерия Лебега имеем, что она непрер почти всюду на Е, значит и |f(x)| непр. почти всюду на E => |f(x)| интегрир. по Р на E. Далее, пусть J 
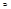E. | | = |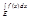 
| = | 
| = 
= 
≤ 
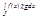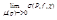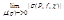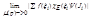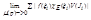= 2) Пусть J 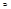E и P-любое разб-е J. тогда если f(x)≥0 то и σ(P,f,χ)≥0, а значит и = 
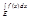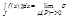≥0. 3) Рассмотрим g(x) – f(x). это выр-е ≥0 по усл-ю для всех x из Е. Применим св-во 2 и получим необх. рез-т.
