Критерий Лебега интегрируемости по множеству. Определение меры Жордана допустимого множества. Внутренняя и внешняя меры Жордана допустимого множества

Трм: f(x): R ^k -> R; Эта функция интегрируема по Риману на допустимом множестве E из R ^k тогда и только тогда, когда она непрерывна почти всюду на E. Д-во: J 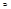E, f(x)χ_E(x) может иметь разрыв на E или на границе. Т.о. получается, что эта функция разрывна только в точках, к-рые в совокупности представляют собой множ-во меры 0. Тогда утверждение нашей теоремы следует из определения интеграла по мн-ву или из критерия Лебега интегрируемости ф-ции многих переменных.

Опр1: Мерой Жордана ограниченного множества EÎ R^k называется величина 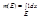. Причём если этот интеграл Римана существует, то существует и мера этого множества ® будем называть множество измеримым по Жордану.

Замечание: Т.к. по определению интеграла по множеству 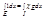, где EÌ I, а множество точек разрыва – множество меры нуль, то, согласно критерию Лебега, введённая мера Жордана определяется только для допустимых множеств.

Опр2: Внутренняя и внешняя меры Жордана допустимого множества Е вводятся как внутренняя и внешняя соответственно площади множества Е, т.е. внутренняя сумма будет представлять собой 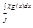, а внешняя - .

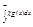[ (Подробно): Пусть J – некоторый промежуток, целиком содержащий в себе Е. тогда для для χ_Е(х) составим s(P, χ) = 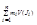и S(P, χ) = 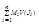; (где m и M - infχ_Е(J_i) и suprχ_Е(J_i) – соответственно). Тогда s – будет представлять собой площадь вписанного, а S – площадь описанного многоугольников. Пределы s и S – существуют, они равны 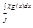и 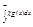и представляют собой внутреннюю и внешнюю площади Е. ]