Теорема о повторном интегрировании для двойного интеграла

ТРМ: Пусть J = {(x₁, x₂)| a≤x₁≤b, c≤x₂≤d} – промежуток в R ² и ф-ция f(x):(J R ²)-> R интегрир. по Р. на этом промежутке и 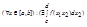тогда справедливо: 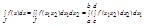= 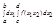Д-во: Введем Ф(x₁), удовл-ю нер-вам: 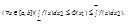Произведем разб-е P₁ отрезка [a,b] на n равных промежутков точками: a=x₁⁰<x₁¹<x₁²<x₁³<...<x₁ⁿ=b. Δx₁ⁱ=x₁ⁱ-x₁^i-1 = (b-a)\n = h. Возьмем разб-е P₂: c=x₂⁰<x₂¹<x₂²<x₂³<...<x₂ⁿ=d, Δx₂ⁱ=x₂ⁱ-x₂^i-1 = (d-c)\n = k. Причем понятно, что h и k стремятся к 0 при n->+ 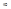; 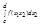сущ-т при 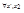; Составим S и s. Имеем s(P₂,f)≤Ф(x₁) ≤S(P₂,f); P=P₁xP₂; s(P,f)≤∑Ф(ξ_i)Δx₁ⁱ ≤S(P,f); Перейдем к пределу. В виду существования двойного интеграла, обе суммы будут стермится к нему, а значит и lim∑Ф(ξ_i)Δx₁ⁱ -> 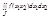; Т.е. двойной интеграл 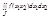представляет собой и интеграл от ф-ции Ф(x₁): 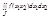= = 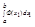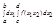чтд.