Теорема о среднем для кратного интеграла

ТРМ: Пусть заданы f(x): R ^k -> R и g(x): R ^k -> R. E – допустим. мн-во. Тогда 1) Если f(x) и g(x) интегрир. и g(x) – знакопост. (пусть для опред-ти g(x)≥0) и m≤f(x)≤M тогда сущ-ет такое m≤µ≤M что вып-ся 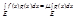2) E – допустим. и связное и f(x) 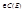. Тогда сущ-ет ξ из Е такая, что выполняется: 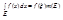. Д-во: 1) из условия интегрир-ти по Р f(x) и g(x) следует что и f(x)*g(x) также интегр. на Е. В самом деле, согласно критерия Лебега, для любых f(x) и g(x) множ-во точек разрыва имеет меру 0. Тогда и [f(x)*f(x)] имеет мн-во точек разрыва меры 0, значит [f(x)*f(x)] интегрир. на допустимом мн-ве E. Умножим нер-во m≤f(x)≤M на g(x)≥0. Имеем mg(x)≤f(x)*g(x)≤Mg(x). Используя св-ва инт-в имеем: 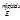≤ ≤ 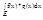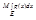. Т.к. g(x)≥0 то и 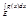≥0. Если 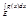=0 тогда в качестве µ подойдет любое число из [m,M] и трм. доказ. Если 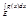>0; Разделим: m≤ 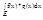/ 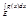≤M и за µ возьмем 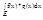/ 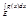. Трм. доказ. 2) Поскольку f(x) непрерывна на E по условию, то она 1)интегрир. по Р на Е и 2)в силу 1й и 2й трм Вейерштрасса о непрер. ф-циях мыв получим что m≤f(x)≤M, где m=inf f(x), M=supr f(x), x E. и по 2й трм. Вейерштрасса эти знач-я достиг-ся, т.е. m=f(x₁), M=f(x₂). если в предыдущем пункте положить g(x)≡1 для x E, имеем 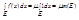. В силу 2й трм Вейерштр, 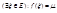. тогда получаем, что 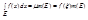, чтд.