I. Ряды. Уравнения математической физики.
I. Числовые ряды.
Среди достаточных признаков сходимости рядов с положительными членами наиболее эффективным является интегральный признак Коши. Поэтому, если другие признаки (1 и 2 признаки сравнения, признаки Коши и Даламбера) не позволяют решить вопрос о сходимости или расходимости числового ряда с положительными членами, то следует прибегнуть, если это возможно, к интегральному признаку Коши.
Пример: Исследовать на сходимость ряд 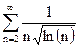

Решение: Воспользуемся признаком Даламбера. По условию 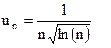
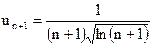 , следовательно
, следовательно 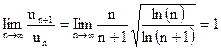 , т.е. признак Даламбера не позволяет сделать заключение о сходимости или расходимости ряда. Поэтому используем интегральный признак Коши. Члены данного ряда положительны и убывают. В качестве функции
, т.е. признак Даламбера не позволяет сделать заключение о сходимости или расходимости ряда. Поэтому используем интегральный признак Коши. Члены данного ряда положительны и убывают. В качестве функции 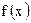 , о которой идет речь в интегральном признаке,
, о которой идет речь в интегральном признаке,
возьмем 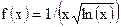 при
при 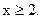 Эта функция непрерывна и убывает,
Эта функция непрерывна и убывает,
причем 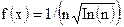 Так как несобственный интеграл
Так как несобственный интеграл
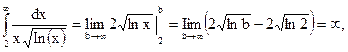 то данный ряд расходится.
то данный ряд расходится.
Вопросы для самопроверки.
1. Дайте определения сходящегося и расходящегося рядов. Исследуйте сходимость ряда, составленного из членов геометрической прогрессии.
2. Докажите необходимый признак сходимости ряда.
3. Докажите, что отбрасывание конечного числа членов ряда не изменяет его сходимости (расходимости). Покажите, что сумма ряда равна сумме первых его n членов, сложенной с суммой остатка ряда.
4. Докажите признаки сравнения рядов с положительными членами. Приведите примеры применения этих признаков.
5. Докажите признак Даламбера сходимости знакоположительных рядов. Приведите пример применения этого признака.
6. Докажите признак Коши сходимости рядов с положительными членами. Приведите примеры применения этого признака.
7. Докажите интегральный признак сходимости ряда Коши. Приведите пример применения этого признака.
8. Дайте определение абсолютно сходящегося ряда. Докажите, что из абсолютной сходимости ряда следует его сходимость. Сформулируйте свойства абсолютно сходящихся рядов. Приведите примеры абсолютно и условно сходящихся рядов.
9. Докажите признак Лейбница сходимости знакочередующихся рядов. Приведите пример на применения этого признака. Покажите, что при замене суммы ряда типа Лейбница суммой первых его членов допускаемая абсолютная погрешность не превосходит модуля первого отброшенного члена.
2. Функциональные и степенные ряды. Приложение
степенных рядов к приближенным вычислениям.
Следует отметить два метода отыскания частного решения дифференциального уравнения по заданным начальным условиям в виде ряда Тейлора: последовательного дифференцирования и неопределенных коэффициентов. Сумму конечного числа членов этого ряда можно принять за приближенное решение дифференциального уравнения.
Вопросы для самопроверки.
1. Дайте определение области сходимости функционального ряда. Приведите примеры рядов с различными областями сходимости.
2. Дайте определение понятия равномерной сходимости последовательности функций. Какой ряд называется равномерно сходящимся?
3. Сформулируйте признак Вейерштрасса абсолютной и равномерной сходимости ряда.
4. Сформулируйте основные свойства равномерно сходящихся рядов.
5. Докажите теорему Абеля о сходимости степенных рядов.
6. Выведите формулу для вычисления радиуса сходимости степенного ряда.
7. Разложите функцию 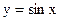 в степенной ряд и докажите с помощью остаточного члена сходимость полученного ряда к данной функции.
в степенной ряд и докажите с помощью остаточного члена сходимость полученного ряда к данной функции.
8. Разложите функцию 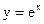 в степенной ряд и докажите с помощью остаточного члена сходимость полученного ряда к данной функции.
в степенной ряд и докажите с помощью остаточного члена сходимость полученного ряда к данной функции.
9. Разложите функцию 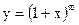 в степенной ряд и найдите интервал сходимости полученного ряда.
в степенной ряд и найдите интервал сходимости полученного ряда.
10. Приведите пример оценки точности вычисления суммы знакочередующего ряда.
11. Приведите пример применения остаточного члена формулы Тейлора (в форме Лагранжа) к оценки точности вычисления с помощью степенного ряда.
12. Изложите метод приближенного интегрирования дифференциальных уравнений с помощью степенных рядов. Приведите пример.
3. Ряды Фурье.
Тригонометрические ряды играют важную роль в математике как аппарат изучения функций. Это объясняется тем, что для разложения в тригонометрический ряд функция не должна удовлетворять столь жестким требованиям, которые предъявляются к ней при разложении, например, в степенной ряд (в степенные ряды разлагаются даже не все бесконечно дифференцируемые функции). Велико значение тригонометрических рядов в приложениях, где их применяют при решении ряда задач математической физики, в электротехнике, метрологии и т. д. Чаще всего ряды Фурье используют при изучении периодических процессов.
Вопросы для самопроверки
1. Выведите формулы для коэффициентов ряда Фурье.
2. Сформулируйте достаточные условия разложимости функции в ряд Фурье. Приведите примеры функций, удовлетворяющих и не удовлетворяющих этим условиям.
3. Выведите формулы для коэффициентов ряда Фурье для четных и не четных функций.
4. Представьте ряд Фурье в комплексной форме.
4. Уравнение математической физики.
К решению волнового уравнения сводятся задачи о поперечных колебаниях струны и продольных колебаниях стержней, о звуковых и электромагнитных колебаниях, о колебаниях газа и многие другие задачи о распространении колебаний в однородной среде. К решению уравнения теплопроводности сводятся задачи о распространении тепла в однородной среде, о фильтрации жидкостей или газов и др. задачи.
Пример. Найти решение уравнения с частными производными
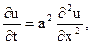
удовлетворяющее краевым условиям: 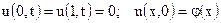
Решение: Пользуясь методом Фурье, полагаем 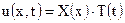
Тогда заданное уравнение преобразуется к виду 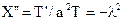 и распадается на два уравнения
и распадается на два уравнения 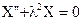 и
и 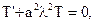 решая которые, найдем
решая которые, найдем 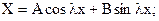
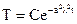
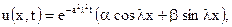 где
где 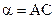 и
и 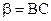 - произвольные постоянные.
- произвольные постоянные.
Используя условие 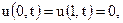 получим
получим 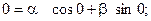
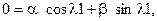 откуда следует:
откуда следует: 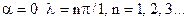
Каждому значению 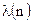 соответствует частное решение
соответствует частное решение
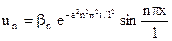
сумма которых 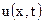 также будет решением данного уравнения
также будет решением данного уравнения
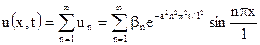 (
(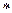 )
)
Используя условие 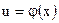 при
при 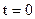 , получим для определения
, получим для определения 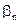 равенство
равенство
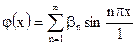
Это равенство есть разложение в интервале (0, 1) данной функции 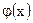 в неполный ряд Фурье, содержащий только синусы. Поэтому
в неполный ряд Фурье, содержащий только синусы. Поэтому
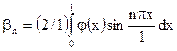 (**)
(**)
Таким образом, сумма ряда (*), коэффициенты которого определяются формулами (**), есть частное решение данного уравнения, удовлетворяющее данным краевым условиям.
Вопросы для самопроверки.
1. Дайте классификацию уравнений с частными производными второго порядка. Приведите примеры.
2. Выведите уравнение колебаний струны. Сформулируйте краевую задачу о колебаниях струны, закрепленной на концах.
3. Изложите метод Фурье нахождения решения краевой задачи о колебаниях струны, закрепленной на концах.
4. Выведите уравнение распространения теплоты в стержне. Сформулируйте краевую задачу.
5. Изложите метод Фурье для нахождения решения уравнения теплопроводности.
 2015-05-13
2015-05-13 493
493








