1. Числовой ряд исследовать на абсолютную и условную сходимость. Для функционального ряда найти область сходимости и исследовать на границе области.*
а) 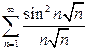
| б) 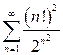
| в) 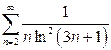 
| |
г) 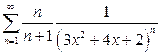
| д) 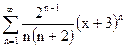
| ||
а) 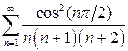
| б) 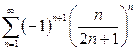
| в) 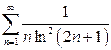 
| |
г) 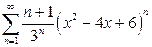
| д) 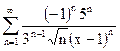
| ||
а) 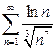
| б) 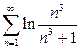
| в) 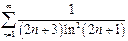 
| |
г) 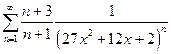
| д) 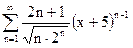
| ||
а) 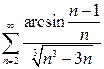
| б) 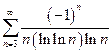
| в) 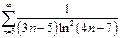 
| |
г) 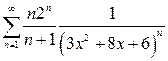
| д) 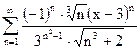
| ||
а) 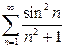
| б) 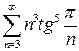
| в) 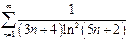 
| |
г) 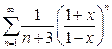
| д) 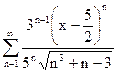
| ||
а) 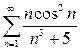
| б) 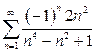
| в) 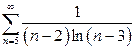 
| |
г) 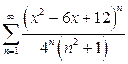
| д) 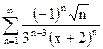
| ||
а) 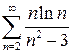
| б) 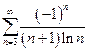
| в) 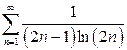 
| |
г) 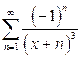
| д) 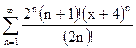
| ||
а) 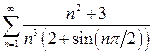
| б) 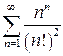
| в) 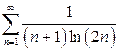 
| |
г) 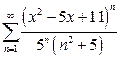
| д) 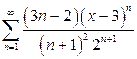
| ||
а) 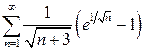
| б) 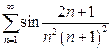
| в) 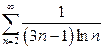 
| |
г) 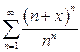
| д) 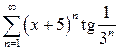
| ||
а) 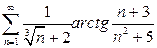
| б) 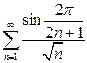
| в) 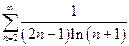 
| |
г) 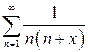
| д) 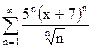
| ||
а) 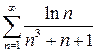
| б) 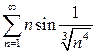
| в) 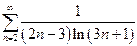 
| |
г) 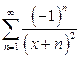
| д) 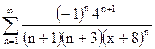
| ||
а) 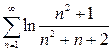
| б) 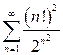
| в) 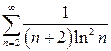 
| |
г) 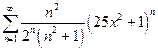
| д) 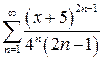
| ||
а) 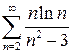
| б) 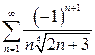
| в) 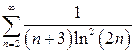 
| |
г) 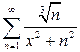
| д) 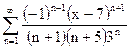
| ||
а) 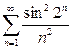
| б) 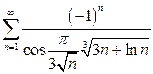
| в) 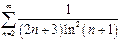 
| |
г) 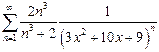
| д) 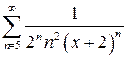
| ||
а) 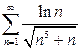
| б) 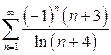
| в) 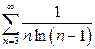 
| |
г) 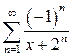
| д) 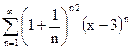
| ||
а) 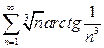
| б) 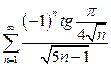
| в) 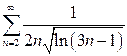 
| |
г) 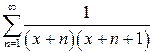
| д) 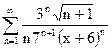
| ||
а) 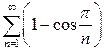
| б) 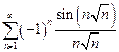
| в) 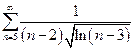 
| |
г) 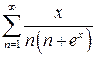
| д) 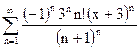
| ||
а) 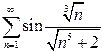
| б) 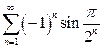
| в) 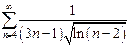 
| |
г) 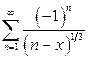
| д) 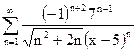
| ||
а) 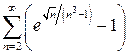
| б) 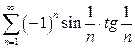
| в) 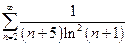 
| |
г) 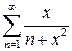
| д) 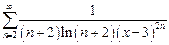
| ||
а) 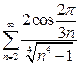
| б) 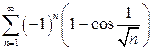
| в) 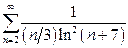 
| |
г) 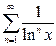
| д) 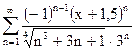
| ||
а) 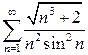
| б) 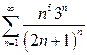
| в) 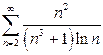 
| |
г) 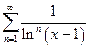
| д) 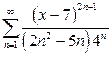
| ||
а) 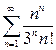
| б) 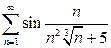
| в) 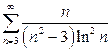 
| |
г) 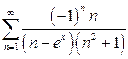
| д) 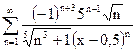
| ||
а) 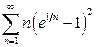
| б) 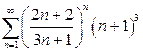
| в) 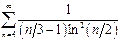 
| |
г) 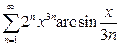
| д) 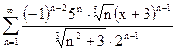
| ||
а) 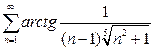
| б) 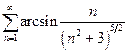
| в) 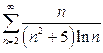 
| |
г) 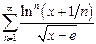
| д) 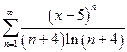
|
2. Найти сумму ряда.*
а) 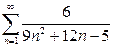
| б) 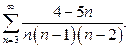
| |
в) 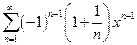
| г) 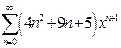
| |
а) 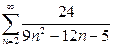
| б) 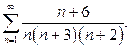
| |
в) 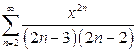
| г) 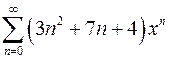
| |
а) 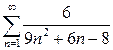
| б) 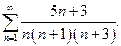
| |
в) 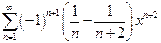
| г) 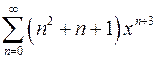
| |
а) 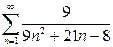
| б) 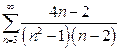
| |
в) 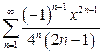
| г) 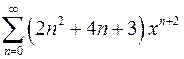
| |
а) 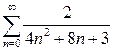
| б) 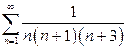
| |
в) 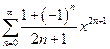
| г) 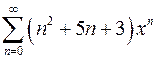
| |
а) 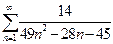
| б) 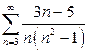
| |
в) 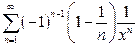
| г) 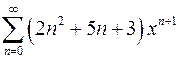
| |
а) 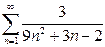
| б) 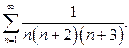
| |
в) 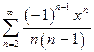
| г) 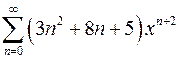
| |
а) 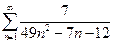
| б) 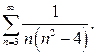
| |
в) 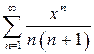
| г) 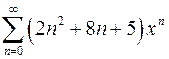
| |
а) 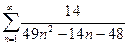
| б) 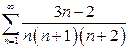
| |
в) 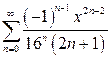
| г) 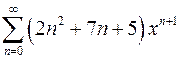
| |
а) 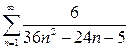
| б) 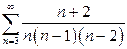
| |
в) 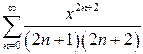
| г) 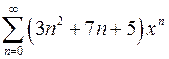
| |
а) 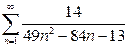
| б) 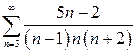
| |
в) 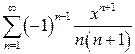
| г) 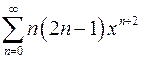
| |
а) 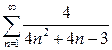
| б) 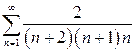
| |
в) 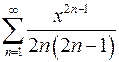
| г) 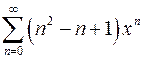
| |
а) 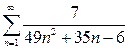
| б) 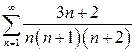
| |
в) 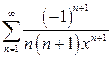
| г) 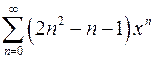
| |
а) 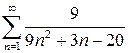
| б) 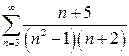
| |
в) 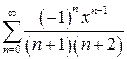
| г) 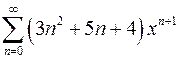
| |
а) 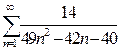
| б) 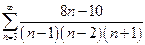
| |
в) 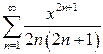
| г) 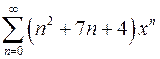
| |
а) 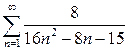
| б) 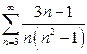
| |
в) 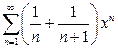
| г) 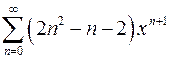
| |
а) 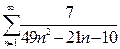
| б) 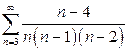
| |
в) 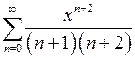
| г) 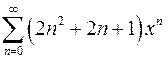
| |
а) 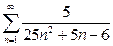
| б) 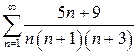
| |
в) 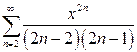
| г) 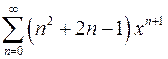
| |
а) 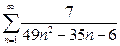
| б) 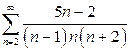
| |
в) 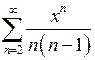
| г) 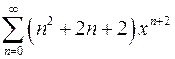
| |
а) 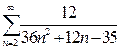
| б) 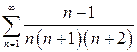
| |
в) 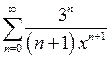
| г) 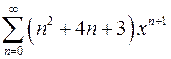
| |
а) 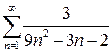
| б) 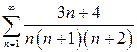
| |
в) 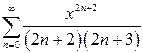
| г) 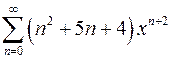
| |
а) 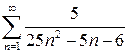
| б) 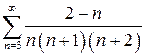
| |
в) 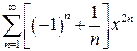
| г) 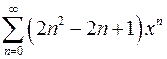
| |
а) 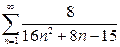
| б) 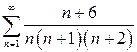
| |
в) 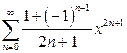
| г) 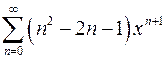
| |
а) 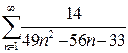
| б) 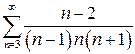
| |
в) 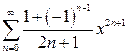
| г) 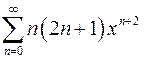
|
3. Найти три первых, отличных от нуля члена разложения в степенной ряд решения 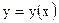 дифференциального уравнения
дифференциального уравнения 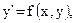 удовлетворяющего начальному условию
удовлетворяющего начальному условию 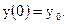
1) 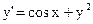 ; ;
| 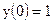
| 2) 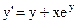 ; ;
| 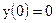
|
3) 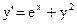 ; ;
| 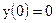
| 4) 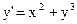 ; ;
| 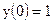
|
5) 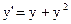 ; ;
| 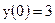
| 6) 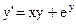 ; ;
| 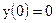
|
7) 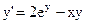 ; ;
| 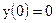
| 8) 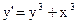 ; ;
| 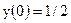
|
9) 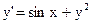 ; ;
| 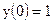
| 10) 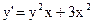 ; ;
| 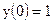
|
11) 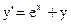 ; ;
| 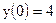
| 12) 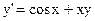 ; ;
| 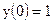
|
13) 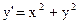 ; ;
| 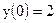
| 14) 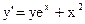 ; ;
| 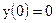
|
15) 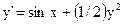 ; ;
| 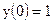
| 16) 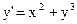 ; ;
| 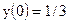
|
17) 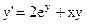 ; ;
| 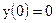
| 18) 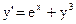 ; ;
| 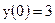
|
19) 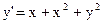 ; ;
| 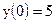
| 20) 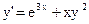 ; ;
| 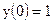
|
21) 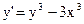 ; ;
| 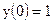
| 22) 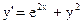 ; ;
| 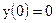
|
23) 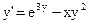 ; ;
| 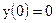
| 24) 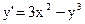 ; ;
| 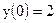
|
4. Разложить в ряд Фурье функцию 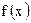 на указанном интервале
на указанном интервале 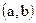 .*
.*
1) 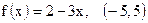 ; ;
| 2) 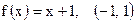
|
3) 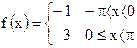 ; ; 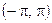
|
4) 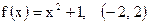
|
5) 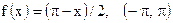 ; ;
| 6) 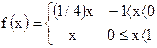 ; ; 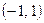
|
7) 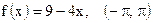 ; ;
| 8) 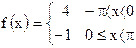 ; ; 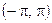
|
9) 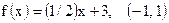 ; ;
| 10) 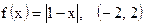 ; ;
|
11) 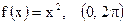 ; ;
| 12) 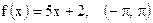 ; ;
|
13) 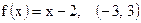 ; ;
| 14) 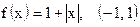 ; ;
|
15) 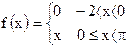 ; ; 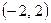
| 16) 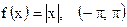 ; ;
|
17) 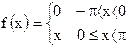 ; ; 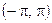
| 18) 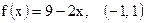 ; ;
|
19) 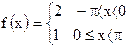 ; ; 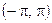
| 20) 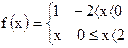 ; ; 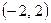
|
21) 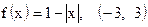 ; ;
| 22) 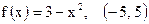 ; ;
|
23) 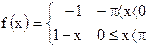 ; ; 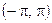
| 24) 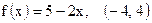
|
5. Методом Фурье решить уравнение колебаний конечной струны длины 1 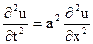 с граничными условиями
с граничными условиями 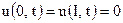 и начальными условиями
и начальными условиями 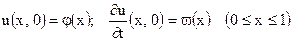
1) 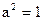
| ; 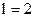
| ; 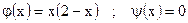
|
2) 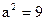
| ; 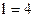
| ; 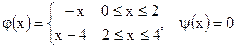
|
3) 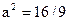
| ; 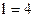
| ; 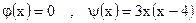
|
4) 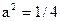
| ; 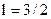
| ; 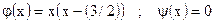
|
5) 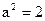
| ; 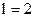
| ; 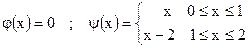
|
6) 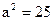
| ; 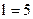
| ; 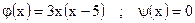
|
7) 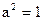
| ; 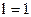
| ; 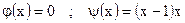
|
8) 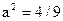
|
; 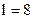
|
; 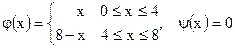
|
9) 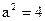
| ; 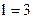
| ; 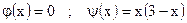
|
10) 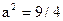
| ; 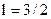
| ; 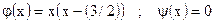
|
11) 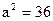
| ; 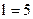
| ; 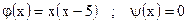
|
12) 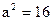
| ; 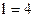
| ; 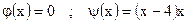
|
Методом Фурье решить уравнение теплопроводности стержня длины l 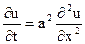 (найти распределение тепла в любой момент времени t вдоль стержня, имеющего теплопроницаемую боковую поверхность) с граничными условиями
(найти распределение тепла в любой момент времени t вдоль стержня, имеющего теплопроницаемую боковую поверхность) с граничными условиями 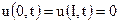
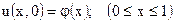 .
.
13) 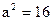
| ; 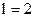
| ; 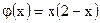
|
14) 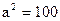
| ; 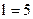
| ; 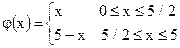
|
15) 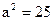
| ; 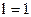
| ; 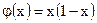
|
16) 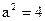
| ; 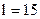
| ; 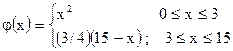
|
17) 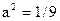
| ; 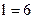
| ; 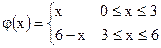
|
18) 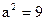
| ; 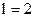
| ; 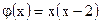
|
19) 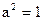
| ; 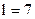
| ; 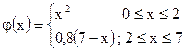
|
20) 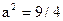
| ; 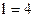
| ; 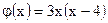
|
21) 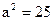
| ; 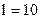
| ; 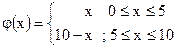
|
22) 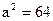
| ; 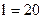
| ; 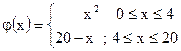
|
23) 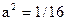
| ; 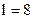
| ; 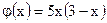
|
24) 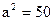
| ; 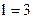
| ; 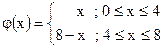
|
 2015-05-13
2015-05-13 478
478








