Касательные напряжения при плоском поперечном изгибе

(формула Д.И.Журавского для τ)

При плоском поперечном изгибе в сечении балки возникают как нормальные (s), так и касательные (t) напряжения, равнодействующими которых являются изгибающий момент (М) и поперечная сила (Q), соответственно.

Рассмотрим простую балку в состоянии плоского поперечного изгиба.

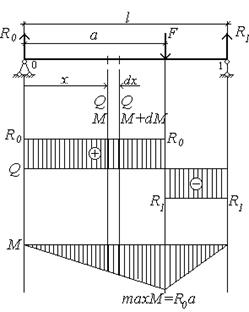
Рис.4.22

Выделим элемент балки длиной dx на расстоянии х от опоры 0. В левом сечении балки, согласно методу сечений, действуют положительные поперечная сила Q и изгибающий момент М, в правом сечении – поперечная сила Q и изгибающий момент М + dМ. В левом и правом сечениях на расстоянии у₁ от главной центральной оси z выделим, симметрично относительно оси у, элементарные площадки с площадью dA и приложим к ним нормальные и касательные напряжения, соответствующие действующим внутренним усилиям. Также как и момент М, нормальные напряжения в правом сечении будут больше, чем в левом, на величину ds.

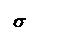
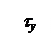
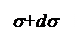
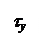
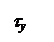
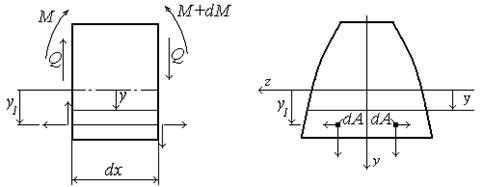
Рис.4.23

Заметим, что наряду с касательными напряжениями t_у, в сечениях будут действовать также касательные напряжения t_z. Однако, у балок, сечения которых симметричны относительно оси у, что имеет место при плоском поперечном изгибе, эти напряжения малы и распределены по сечению симметрично относительно оси у (см. рис.4.23), поэтому ими пренебрегают. Также заметим, что напряжения t_z играют существенную роль при расчете балок из тонкостенных несимметричных профилей.

Определим напряжения t_y (индекс «у» у напряжений в дальнейшем будем опускать). Для этого плоскостью, параллельной нейтральному слою, расположенной от него на расстоянии у, рассечем элемент и рассмотрим равновесие нижней его части (рис.4.24).

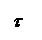
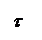
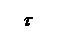
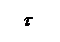
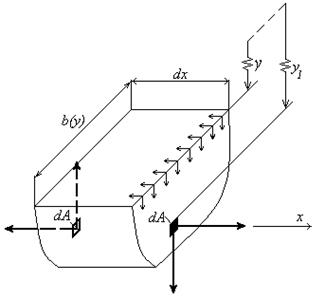
Рис.4.24

Согласно закону парности касательных напряжений, по площади горизонтального сечения, перпендикулярно ребру, будут действовать касательные напряжения, которые равны по величине касательным напряжениям t, действующим в поперечном сечении на уровне у. Обозначим через А₁ – площадь части поперечного сечения, расположенной ниже уровня горизонтального сечения (у).

Используем следующие допущения:

1) касательные напряжения равномерно распределены по ширине сечения;

2) при определении t будем пользоваться формулой для s, полученной при чистом изгибе;

3) продольные волокна балки не надавливаются друг на друга (s_y =0).

Заметим, что по длине элемента dx, из-за ее малости, напряжения t также распределены равномерно.

Запишем уравнение равновесия для проекций сил на ось х

.

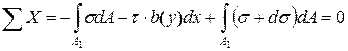Здесь интегралы представляют собой равнодействующие нормальных напряжений s, которые прикладываются по площади А₁ левого и правого поперечных сечений. Приводя в полученном уравнении подобные члены, выразим искомые касательные напряжения. При этом внесем под знак интеграла длину элемента dx, как величину, не зависящую от переменной интегрирования. В результате получим

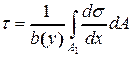. (4.9)

Выполним в этом соотношении ряд преобразований и подстановок. Представим интеграл в виде 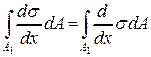, куда подставим выражение для нормальных напряжений, записанное согласно принятому допущению 2. В результате будем иметь

.

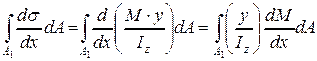Напомним, что второе дифференциальное соотношение Журавского имеет вид 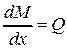, где Q – поперечная сила в сечении. С учетом этого, рассматриваемый интеграл запишется в форме

.

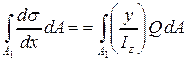Вынесем за знак интеграла величины, которые не зависят от переменной интегрирования, и подставим полученное выражение в формулу (4.9)

.

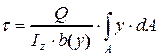Здесь: 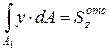- статический момент относительно главной центральной оси z отсеченной части площади поперечного сечения А₁. С учетом этого формула для касательных напряжений t при ППИ (формула Д.И.Журавского) принимает вид

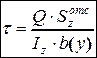(4.10)

Напомним обозначения, входящие в формулу Журавского:

Q – поперечная сила в сечении, в котором определяются напряжения t;

I_z – момент инерции поперечного сечения относительно оси z;

b(y) – ширина сечения на уровне, где определяется напряжения;

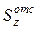– статический момент относительно оси z части площади, которая лежит либо выше (А^отсВ), либо ниже (А^отсН) уровня, где определяются касательные напряжения t (см. рис.4.25).

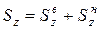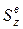Последнее положение требует пояснения. Согласно теореме сложения, статический момент всего поперечного сечения относительно оси z равен , где и 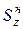статические моменты верхней и нижней частей сечения относительно оси z.

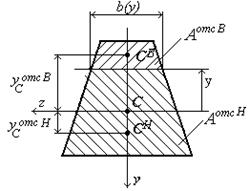
Рис.4.25

С другой стороны, поскольку ось z является центральной, 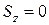. Отсюда следует 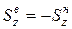. В формулу Журавского подставляется абсолютная величина рассматриваемых статических моментов, т. 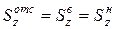е. , где

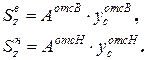
В этих формулах: 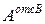, 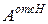- площади верхней и нижней частей сечения; 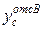, 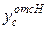- расстояния от оси z до центра тяжести верхней и нижней частей сечения.

Отметим, что знак касательных напряжений, вычисляемых по формуле Журавского, определяется только знаком поперечной силы Q.