Задача 8. Исследовать переходный процесс в системе «Четырехполюсник с емкостным элементом на входе» при подаче на вход ступенчатого возмущения

Исследовать переходный процесс в системе «Четырехполюсник с емкостным элементом на входе» при подаче на вход ступенчатого возмущения.

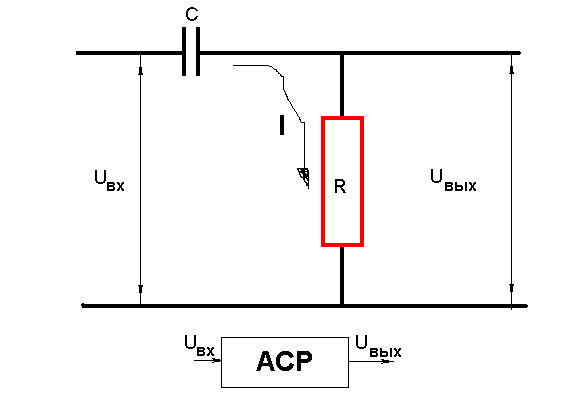
Рисунок 1 к задаче 8.

Положим, что до прихода возмущения в системе «Четырехполюсник с емкостным элементом» входное и выходное напряжения равнялись нулю.

Выразим связь выходного и входного напряжений, пользуясь законами Ома и Кирхгофа, для чего запишем систему, описывающую падения напряжений на участках цепи:

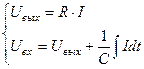
Выразив ток I из первого уравнения системы, подставив полученное выражение во второе уравнение и продифференцировав второе уравнение, получим:

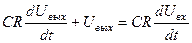. Подставим вместо : .

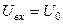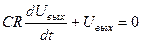Характеристическое уравнение 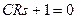имеет единственный действительный корень - 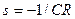. Общее решение ОЛДУ, оно же – функция, описывающая переходный процесс при скачкообразном возмущении на входе - 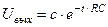. Найдем значение постоянной интегрирования с из начальных условий: 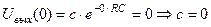. Таким образом получаем нулевое решение уравнения при подаче на вход скачкообразного напряжения. Сопоставим результат с физическим опытом – действительно, емкость на входе в цепь ведет себя как «барьер», преодолеть который возможно, только подавая на вход напряжения, изменяющиеся во времени.