Типовые импульсные воздействия

При исследовании динамических свойств линейных цепей и си­стем в качестве типовых элементарных воздействий обычно ис­пользуется единичная ступенчатая функция 1(t) и дельта-функ­ция δ(t).

Единичная ступенчатая функция l(t), называемая также функ­цией Хевисайда или функцией включения (рис. 14.3, а), имеет зна­чения:

иобычно неопределенна при t=0.

При смещении такой функции вправо по оси абсцисс на время τ(рис, 14,3, б) ее можно выразить в виде

Возникновение ступенчатых сигналов весьма типично. В теории цепей они соответствуют, например, включению постоянного на­пряжения на вход устройства при замыкании ключа. Если цепь включается в момент t=t₀ на напряжение u(t), то это соответ­ствует воздействию вида f(t)=u(t) · l (t—t₀) (рис. 14.4),

С помощью единичных ступенчатых функций можно предста­вить большое число разнообразных сигналов. Например, прямо­угольный импульс можно описать (рис. 14.5, а)разностью

.

а более сложный сигнал — суммой п ступенчатых функций (рис. 14.5,6)

где

Дельта-функция δ(t), или функция Дирака, может быть пред­ставлена по-разному. С точки зрения инженера, желающего ви-

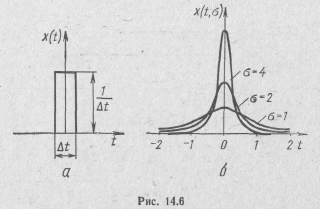
деть δ (t) -функцию как сигнал в физической системе, функция Ди­рака представляет импульс с бесконечно большой амплитудой и бесконечно малой длительностью, площадь которого конечна и равна единице. В качестве при­мера представим импульс сколь угодно малой длительности Δt, амплитуда которого (рис. 14.6, а). В пределе, когда , его амплитуда , но площадь остается постоянной и равна U_mΔt =l.

Такое определение δ(t)-функ­ции, несмотря на его простоту и наглядность, не является строгим в математическом отношении. Тем не менее оно достаточно для боль­шинства приложений, встречающихся в теории электрорадио цепей.

Более строго в этом отношении δ(t)-функция определяется как предел рав­номерно сходящейся последовательности непрерывных функций. Например, последовательность непрерывных функций (рис. 14.6,6)

сходится к нулю при . При t = 0 и значения этих функций неогра­ниченно возрастают.

Анал о гичн о о пределяют и единичную ступенчатую функцию 1 (t). Например, последовательность непрерывных функций (рис. 14.7)

(14.8)

при t<О имеет предел 0, а при t>0 ее пределом является 1, что соответствует выражению (14.3).

Дельта функция, как и функция l(t), относится к специаль­ному типу функций, имеющих определенные свойства и называе­мых обобщенными функциями.

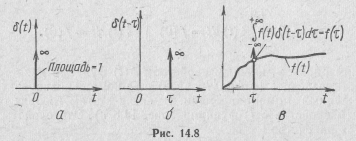
Для δ(t)-функции (рис. 14.8, α) справедливы соотношения:

При смещении δ (t) -функции вправо по оси абсцисс на время τ (рис. 14.8,6) получим:

В практическом отношении ценность δ(t)-функции заключается в конечном значении ее площади, чего нельзя сказать о конкрет­ном значении самой функции.

Важность δ(t)-функции становится более ясной при интегри­ровании. Более ценными являются не значения самой δ(t)-функ­ции, а то, что с ней происходит при интегрировании. Это особенно проявляется при решении часто встречающихся на практике задач, связанных с воздействиями кратковременных толчков или им­пульсов. Результат таких воздействий часто не зависит от формы импульса, а определяется интегральным значением, т. е. площадью импульса.

Рассмотрим интеграл, содержащий произведение произволь­ной непрерывной функции и δ-функции:

Учитывая, что лишь при t=0 и в окрестностях этой точки на бесконечно малом интервале от —Δt до Δt ƒ(t) ƒ(0) (Δt 0), получим

Таким образом, важным свойством б(t)-функции является воз­можность выделить (отфильтровать) с ее помощью значение функ­ции в данный момент времени. В связи с этим говорят о филь­трующем свойстве б (t)-функции (рис. 14.8, в). Это свойство опре­деляется равенством

Если в формулу (14.11) подставить б (t)-функцию, смещенную на произвольный момент времени τ, то аналогично получим равенство для более общего случая

Между единичной ступенчатой функцией l(t) и б(t)-функцией Дирака существует тесная связь:

Действительно, при t<0 функция 6(t) и ее интеграл.равны нулю. После перехода через момент времени t=0 значение инте­грала изменяется скачком на единицу и остается равным единице.

С другой стороны,

так как l^/(t)=0 при f-И-О и V(t)==oo при t=0.

Таким образом, б (t)-функция равна первой производной еди­ничной ступенчатой функции.

Импульсные воздействия, близкие к б (t)-функции, встречаются достаточно часто на практике, например удары в механических системах, броски э. д. с. самоиндукции при коммутациях в электри­ческих цепях и др,