В основе расчета реакции линейной цепи на воздействие произвольной формы с использованием ее временных характеристик лежит принцип наложения. Суть такого метода расчета заклю-
чается в представлении входного воздействия суммой (наложением) простых типовых импульсных функций.
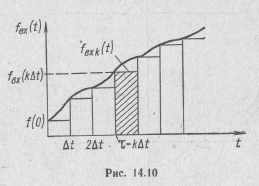
Представим входной сигнал произвольной формы наложением прямоугольных импульсов малой длительности tи=Δτ=Δt (рис. 14.10).
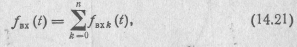
где
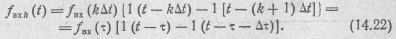
При малой длительности Δτ реакция цепи на каждый импульс 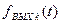 в соответствии с формулой (14.18) определяется с помощью ее импульсной характеристики как произведение:
в соответствии с формулой (14.18) определяется с помощью ее импульсной характеристики как произведение:
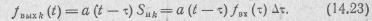
Реакцию цепи на воздействие 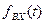 в соответствии с принципом наложения найдем как сумму реакций
в соответствии с принципом наложения найдем как сумму реакций 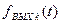 :
:
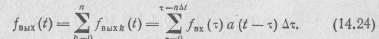
Устремляя Δτ>0, в пределе получаем t
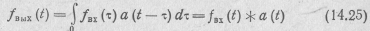
или после замены переменных
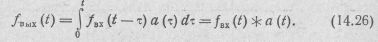
Здесь интегрирование производится по τ, апод t понимают фиксированный момент времени, в который требуется найти значение 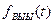 .
.
Полученные выражения называются интегралами свертки. Они позволяют найти реакцию линейной цепи на произвольное воздействие как свертку входного воздействия с импульсной характеристики цепи. Подобные выражения можно получить и при аппроксимации функции воздействия с помощью ступенчатых функций (см. рис. 14.5,6).
Интегралу свертки можно дать графическую интерпретацию. Для этого последовательность свертывания двух функций проиллюстрируем с помощью рис. 14.11. Свертываемые функции (рис. 14.11,а) после замены переменной t на τ (рис. 14.11,6) преобразуем путем замены т на (—τ). Такое преобразование (рис. 14.11,0) соответствует зеркальному отражению функций относительно оси ординат. Последующая замена (—τ) на (t—τ) соответствует смещению отраженных функций вправо на величину t (рис. 14.11,г). Произведение двух функций, находящееся под знаком интеграла в свертке (14.25) и (14.26), представлено на рис. 14.11, д. Интегрирование перемноженных функций дает значение интеграла свертки в данный момент времени (рис. 14.11, е). Ордината результирующей кривой (см. рис. 14.11, е) соответствует площади заштрихованной поверхности (см. рис. 14.11,д). Для нахождения каждой новой ординаты требуется новое отражение и смещение, после чего выполняется перемножение ординат и интегрирование.
Таким образом, свертывание двух функций может быть представлено с помощью четырех действий — отражения, смещения, перемножения и интегрирования, выполняемых в определенной последовательности.
Если подставить в интегралы (14.25) и (14.26) выражение (14.19) и использовать замену переменных, то получим еще
две формы интеграла свертки, которые в теории цепей обычно называют интегралами Дюамеля:
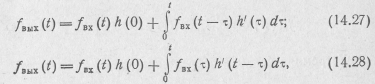
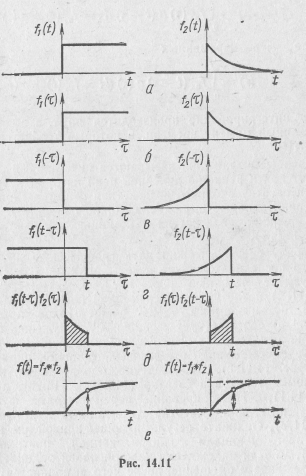
так как
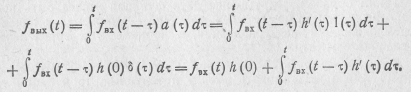
Интегрируя в (14.25) и (14.26) по частям 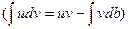 , получаем еще две формы (третью и четвертую) интеграла Дюамеля:
, получаем еще две формы (третью и четвертую) интеграла Дюамеля:
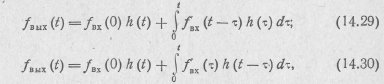
так как
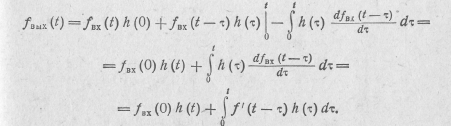
Дифференцируя определенный интеграл (14.25) и (14.26) по верхнему пределу
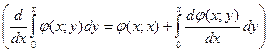
получаем пятую и шестую формы интеграла Дюамеля:
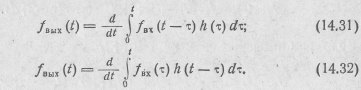
Выбор удобной формы записи интеграла свертки (Дюамеля) определяется условием решаемой задачи, видом входного воздействия и используемой временной характеристики цепи.
Расчет реакции цепи на воздействие произвольной формы распадается в общем случае на два этапа:
расчет временной характеристики нужного вида;
расчет реакции цепи с помощью интеграла свертки (Дюамеля) в любой удобной его форме (14.25) — (14.32).
Пример 14.4.
На вход rC- цепи(см. рис. 14.9, α) п о дается импульс напряжения экспоненциальной формы 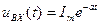 . Определить напряжение на емкости.
. Определить напряжение на емкости.
Решение. 1. Для расчета используем импульсную характеристику
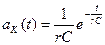
найденную для этой цепи в примере 14.3.
2. С помощью интеграла свертки (14.25) находим напряжение на емкости
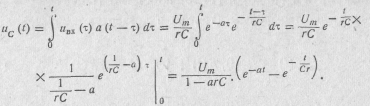
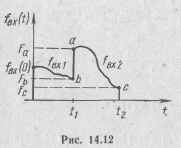 Рассмотрим особенности применения интеграла Дюамеля при сложной форме входного сигнала. Пусть fBX(t) изменяется, например, в соответствии с рис. 14.12. Функция fBX(t) в точках t=0, t1 и t2 изменяется скачком, а на интервалах времени 0— t 1и t 1— t 2 изменяется плавно, но по разным законам: fBX1(t) и fBX2(t) соответственно. Реакцию цепи на такое воздействие, задаваемое на разных интервалах разными функциями и характеризующееся наличием скачков, удобно рассчитать с помощью интеграла Дюамеля ( 14.29) и ( 14.30).
Рассмотрим особенности применения интеграла Дюамеля при сложной форме входного сигнала. Пусть fBX(t) изменяется, например, в соответствии с рис. 14.12. Функция fBX(t) в точках t=0, t1 и t2 изменяется скачком, а на интервалах времени 0— t 1и t 1— t 2 изменяется плавно, но по разным законам: fBX1(t) и fBX2(t) соответственно. Реакцию цепи на такое воздействие, задаваемое на разных интервалах разными функциями и характеризующееся наличием скачков, удобно рассчитать с помощью интеграла Дюамеля ( 14.29) и ( 14.30).
В первом интервале времени: 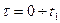
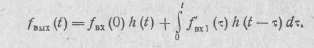
Во втором интервале времени 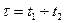
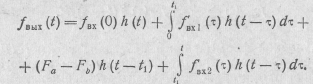
Здесь слагаемое 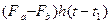 обусловлено скачком вход-юй функции от
обусловлено скачком вход-юй функции от 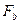 до Fa в момент времени t1.
до Fa в момент времени t1.
В третий интервал времени 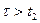
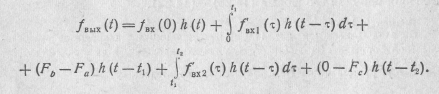
Здесь слагаемое (0-Fc)h(t—t2) обусловлено скачком функции fBX(t) от Fc до 0 в момент времени t2.
14.5. ПОНЯТИЕ О РАСЧЕТЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ
 2015-05-13
2015-05-13 1096
1096
