Метод Гаусса с выбором главного элемента по столбцу

На k- ом шаге прямого хода в качестве ведущего элемента выбирают максимальный по модулю коэффициент 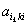при неизвестной 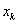в уравнениях с номерами i = k+1,..., m.Затем уравнение, соответствующее выбранному коэффициенту с номером 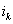, меняют местами с к -ым уравнением системы для того, чтобы главный элемент занял место коэффициента 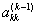. После этой перестановки исключение проводят как в схеме единственного деления. В этом случае все масштабирующие множители по модулю меньше единицы и схема обладает вычислительной устойчивостью.

ПРИМЕР 1.Решение системы методом Гаусса с выбором главного элемента по столбцу.

Пусть Ax=b, где

A = 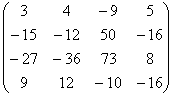, b= .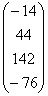

Прямой ход. 1 шаг. Максимальный по модулю элемент 1-го столбца 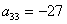. Переставим 1-ое и 3 - е уравнения местами:

A= 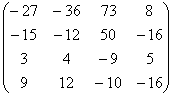, b= .

Вычислим масштабирующие множители 1 шага:

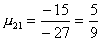
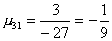
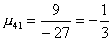
и выполним преобразование матрицы и вектора:

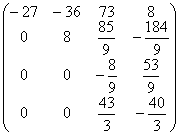A1= b1= .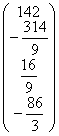

2 шаг. Вычислим масштабирующие множители 2 шага:

.

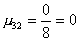
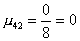Второй шаг не изменяет матриц: A2=A1, b2= b1.

3 шаг. Максимальный по модулю элемент 3 столбца 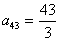. Переставим 3 и 4 уравнения местами.

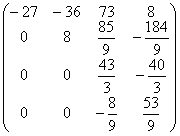A2= b2= .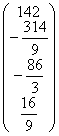

Вычислим масштабирующие множители 3 шага:

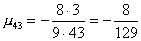
и выполним преобразование матрицы и вектора:

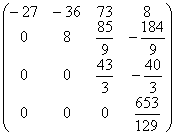A3= b3= .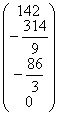

Обратный ход. Из последнего уравнения находим: 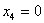. Из третьего

уравнения системы находим 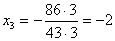. Из второго уравнения находим

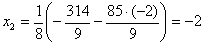. Неизвестное 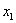находим из первого уравнения:

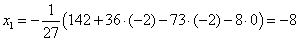
Ответ: .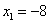

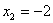
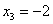
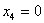% Решить систему Ax=b методом Гаусса

% Введём матрицу

A = [3,4,-9,5;-15,-12,50,-16;-27,-36,73,8;9,12,-10,-16];

% Введём правую часть

b = [-14; 44; 142; -76];

% Решим систему средствами MATLAB

x = A \ b

>>

x =	-8.0000
	-2.0000
	-2.0000
	-0.0000