Метод Холецкого

Если матрица системы является симметричной и положительно определенной, то для решения системы применяют метод Холецкого (метод квадратных корней). В основе метода лежит алгоритм специального LU -разложения матрицы A, в результате чего она приводится к виду A= 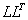. Если разложение получено, то, как и в методе LU -разложения, решение системы сводится к последовательному решению двух систем с треугольными матрицам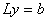и: и 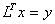. Для нахождения коэффициентов матрицы L неизвестные коэффициенты матрицы 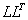приравнивают соответствующим элементам матрицы A. Затем последовательно находят требуемые коэффициенты по формулам:

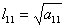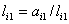, i = 2, 3,..., m,

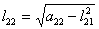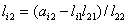, i = 3, 4,..., m,

...............

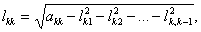
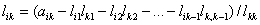i = k+1,..., m.

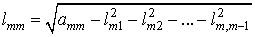
ПРИМЕР 2. Решение системы методом Холецкого.

Пусть

A= 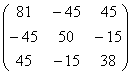b= .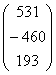

Находим элементы матрицы L:

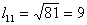
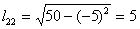
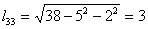
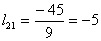
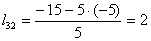
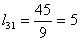
Таким образом, разложение матрицы A имеет вид:

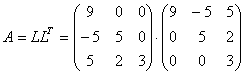
Последовательно решаем системы 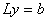и 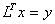. Решением 1-ой системы является вектор 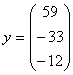, а решение 2-ой системы вектор .

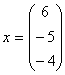Ответ: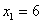

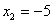
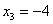
% Решить систему Ax=b методом Холецкого

% Введём матрицу

A = [81 -45 45; -45 50 -15; 45 -15 38];

% Введём правую часть

b = [531; -460; 193];

% Найдём разложение Холецкого

R = chol(A);

% R'*R*x = b

% Матрица R легко обратима

y = R' \ b;

x = R \ y;

% Проверим решение

A * x - b

>>

ans =