Если матрица системы является разреженной, то есть содержит большое число нулевых элементов, то применяют еще одну модификацию метода Гаусса - метод прогонки. Рассмотрим систему уравнений с трехдиагональной матрицей:
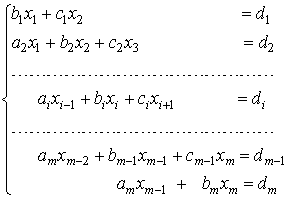
Преобразуем первое уравнение системы к виду 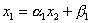 , где:
, где: 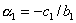 ,
, 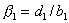 . Подставим полученное выражение во второе уравнение системы и преобразуем его к виду:
. Подставим полученное выражение во второе уравнение системы и преобразуем его к виду: 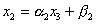 и т.д.
и т.д.
На i -ом шаге уравнение преобразуется к виду: 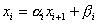 , где
, где 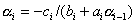 ,
, 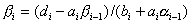 .
.
На m -ом шаге подстановка в последнее уравнение выражения 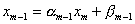
дает возможность определить значение 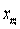 :
:
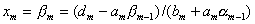 .
.
Значения остальных неизвестных находятся по формулам:
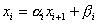 , i = m-1, m-2,..., 1.
, i = m-1, m-2,..., 1.
ПРИМЕР 4. Решение системы методом прогонки.
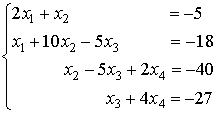
Прямой ход прогонки. Вычислим прогоночные коэффициенты:
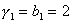 ,
, 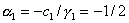 ,
, 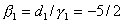
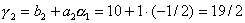 ,
, 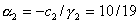
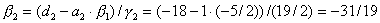
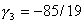 ,
, 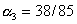 ,
, 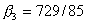
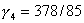 ,
, 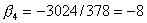
Обратный ход прогонки. Находим значения неизвестных:
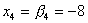 ,
, 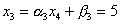 ,
, 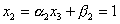 ,
, 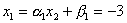
Ответ:
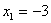
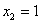
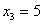
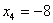 .
.
 2015-05-13
2015-05-13 4383
4383








