Определение параметров эмпирической зависимости

Часто из физических соображений следует, что зависимость 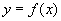между величинами хорошо описывается моделью вида 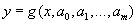, где вид зависимости g известен. Тогда применение критерия наименьших квадратов приводит к задаче определения искомых параметров 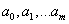из условия минимума функции: .

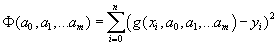ПРИМЕР 3. Вывод нормальной системы уравнений для нахождения параметров эмпирической зависимости.

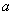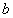Выведем систему уравнений для определения коэффициентов и функции 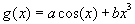, осуществляющей среднеквадратичную аппроксимацию заданной функции 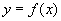по 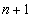точкам. Составим функцию 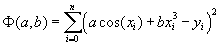и запишем для нее необходимое условие экстремума:

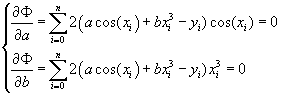
Тогда нормальная система примет вид:

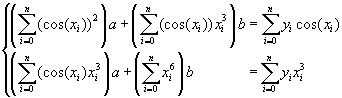
Получили линейную систему уравнений относительно неизвестных параметров, которая легко решается.

Если зависимость от параметров 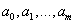нелинейна, то экстремум функции 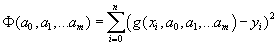ищут методами минимизации функций нескольких переменных.