Постановка задачи интерполяции функций

Пусть функция y = f(x) задана таблицей своих значений:

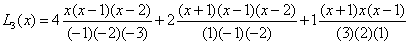, i =0,1,... n. Требуется найти многочлен степени n, такой, что значения функции и многочлена в точках таблицы совпадают:

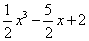, i =0,1,... n.

Справедлива теорема о существовании и единственности интерполяционного многочлена.

Одна из форм записи интерполяционного многочлена - многочлен Лагранжа:

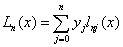, где

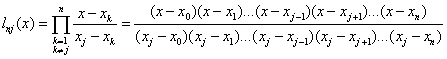
Многочлен 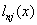представляет собой многочлен степени n, удовлетворяющий условию

.

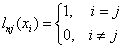Таким образом, степень многочлена 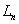равна n и при 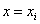в сумме обращаются в нуль все слагаемые, кроме слагаемого с номером 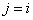, равного 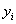. Поэтому многочлен Лагранжа является интерполяционным.

ПРИМЕР 1.Построение многочлена Лагранжа.

По таблице построим интерполяционный многочлен:

x	-1
y

=

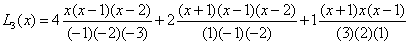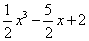
% Построить интерполяционный многочлен Лагранжа

% Введём табличную функцию

x = [-1 0 1 2];

y = [4 2 0 1];

% Построим интерполяционный многочлен (аппроксимация четвёртой степени)

p = polyfit(x, y, 4);

% Коэффициенты интерполяции \sum_{i=0}^n p(i) x^i

p

>>

P =

1.2500

-2.0000

-1.2500

2.0000

Другая форма записи интерполяционного многочлена - интерполяционный многочлен Ньютона с разделенными разностями. Пусть функция f задана с произвольным шагом и точки таблицы занумерованы в произвольном порядке. Величины 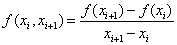называют разделенными разностями первого порядка. Разделенные разности второго порядка определяются формулой:

.

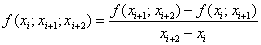Определение разделенной разности порядка 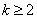таково:

.

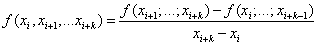Используя разделенные разности, интерполяционный многочлен Ньютона можно записать в следующем виде:

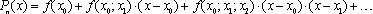
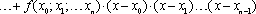
ПРИМЕР 2. Построение интерполяционного многочлена Ньютона с разделенными разностями.

По таблице значений функции из ПРИМЕРА 1 построим интерполяционный многочлен Ньютона. Составим таблицу разделенных разностей:

x	f(x)	f(xi, xi+1)	f(xi, xi+1, xi+2)	f(xi, xi+1, xi+2, xi+23)
-1		-2		1/2
		-2	3/2

Теперь запишем интерполяционный многочлен Ньютона:

/

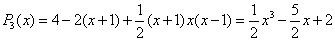Отметим, что в силу единственности интерполяционного многочлена, мы получили тот же самый многочлен, что в ПРИМЕРЕ 1.

Величину 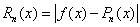называют погрешностью интерполяции или остаточным членом интерполяции.