2015-05-13
992
Если функция n +1 раз на отрезке [ a,b ], содержащем узлы интерполяции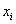 
, i =0,1,... n, то для погрешности интерполяции справедлива оценка:
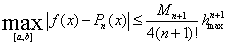. Здесь 
, 
.
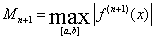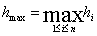Эта оценка показывает, что для достаточно гладкой функции при фиксированной степени интерполяционного многочлена погрешность интерполяции стремится к нулю не медленнее, чем величина, пропорциональная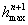 
. Этот факт формулируют так: интерполяционный многочлен степени n аппроксимирует функцию с (n +1) порядком точности относительно 
.
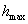ПРИМЕР 3. Использование остаточного члена интерполяции.
Пусть требуется составить таблицу функции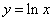 
на отрезке [1,10]. Какой величины должен быть шаг h, чтобы при линейной интерполяции значение функции восстанавливалось с погрешностью не меньшей 
?
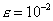Запишем остаточный член интерполяции при линейной интерполяции:
.
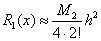Так как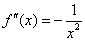 
, то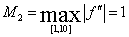 
. Тогда 
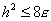. Следовательно, 
.
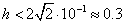В практическом плане формула Ньютона обладает преимуществами перед формулой Лагранжа. Предположим, что в необходимо увеличить степень многочлена на единицу, добавив в таблицу еще один узел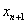 
. При использовании формулы Лагранжа это приводит к необходимости вычислять каждое слагаемое заново. Для вычисления 
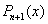достаточно добавить к 
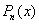лишь очередное слагаемое: 
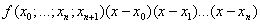. Если функция f достаточно гладкая, то справедливо приближенное равенство 
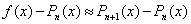. Это равенство можно использовать для практической оценки погрешности интерполяции: 
.
|
|
|
