Метод Эйлера обладает медленной сходимостью, поэтому чаще применяют методы более высокого порядка точности. Второй порядок точности по 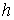 имеет усовершенствованный метод Эйлера:
имеет усовершенствованный метод Эйлера: 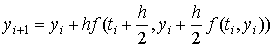 . Этот метод имеет простую геометрическую интерпретацию. Метод Эйлера называют методом ломаных, так как интегральная кривая на отрезке
. Этот метод имеет простую геометрическую интерпретацию. Метод Эйлера называют методом ломаных, так как интегральная кривая на отрезке 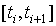 заменяется ломаной с угловым коэффициентом
заменяется ломаной с угловым коэффициентом 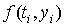 . В усовершенствованном методе Эйлера интегральная кривая на отрезке
. В усовершенствованном методе Эйлера интегральная кривая на отрезке 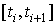 заменяется ломаной с угловым коэффициентом, вычисленным в средней точке отрезка
заменяется ломаной с угловым коэффициентом, вычисленным в средней точке отрезка 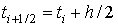 . Так как значение
. Так как значение 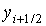 в этой точке неизвестно, для его нахождения используют метод Эйлера с шагом
в этой точке неизвестно, для его нахождения используют метод Эйлера с шагом 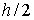 .
.
ПРИМЕР 3. Решение задачи усовершенствованным методом Эйлера.
Выполнить 1 шаг длины 0.4 с использованием усовершенствованного метода Эйлера для решения задачи Коши: 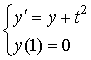 .
.
Зададим шаг 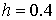 . Тогда решение в точке 1.4 находится так:
. Тогда решение в точке 1.4 находится так:
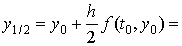
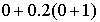 =
= 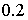
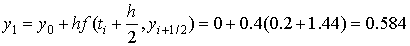
Таким образом 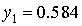 .
.
Еще одна модификация метода Эйлера второго порядка - метод Эйлера-Коши:
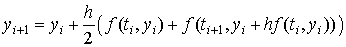
 2015-05-13
2015-05-13 898
898








