Численное решение задачи Коши методом Эйлера

Численное решение задачи Коши состоит в построении таблицы приближенных значений 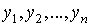в точках 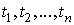. Точки 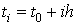, 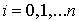называются узлами сетки, а величина 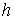- шагом сетки. В основе построения дискретной задачи Коши лежит тот или иной способ замены дифференциального уравнения его дискретным аналогом. Простейший метод основан на замене левой части уравнения правой разностной производной: 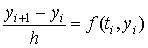. Разрешая уравнение относительно 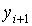, получаем расчетную формулу метода Эйлера: , .

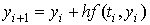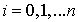ПРИМЕР 1. Решение задачи методом Эйлера.

Применяя метод Эйлера, найти решение задачи Коши: 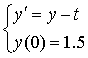в трех последовательных точках 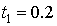, , 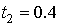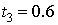. Найти точное решение задачи и найти величину абсолютной погрешности в указанных точках.

Возьмем шаг 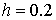. Используя расчетную формулу Эйлера, найдем приближенное решение задачи Коши:

, , .

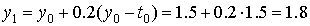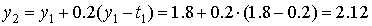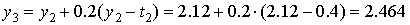Таким образом, получили численное решение задачи Коши с шагом :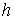

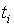		0.2	0.4	0.6
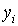	1.5	1.8	2.12	2.464

В этой задаче легко находится точное решение, например, методом вариации постоянной:

. Вычислим значения точного решения в указанных точках.

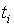		0.2	0.4	0.6
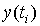	1.5	1.811	2.146	2.511

Абсолютную погрешность вычислим так: 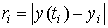. Тогда 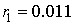, , 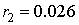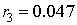. Таким образом, максимальная величина погрешности равна .

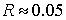Численный метод называется явным, если вычисление решения в следующей точке 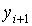осуществляется по явной формуле. Метод называется одношаговым, если вычисление решения в следующей точке 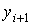производится с использованием только одного предыдущего значения 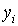. Метод Эйлера является явным одношаговым методом.