Теорема Ролля. Если функция 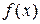 непрерывна на
непрерывна на 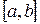 , дифференцируема во всех внутренних точках этого отрезка и на концах
, дифференцируема во всех внутренних точках этого отрезка и на концах 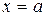 и
и 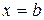 обращается в нуль (т. е.
обращается в нуль (т. е. 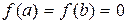 ), то внутри отрезка
), то внутри отрезка 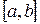 существует, по крайней мере, одна точка
существует, по крайней мере, одна точка 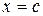 ,
, 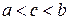 , в которой производная
, в которой производная 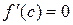 .
.
Теорема Лагранжа. Если функция 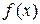 непрерывна на отрезке
непрерывна на отрезке 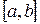 и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка
и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка 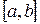 найдется, по крайней мере, одна точка
найдется, по крайней мере, одна точка 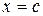 ,
, 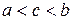 , что
, что
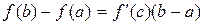 .
.
Теорема Коши. Если 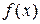 и
и 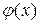 – две функции, непрерывные на отрезке
– две функции, непрерывные на отрезке 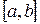 и дифференцируемые внутри него, причем
и дифференцируемые внутри него, причем 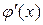 нигде не обращается в нуль внутри этого отрезка, то внутри отрезка
нигде не обращается в нуль внутри этого отрезка, то внутри отрезка 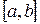 найдется такая точка
найдется такая точка 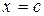 ,
, 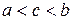 , что
, что
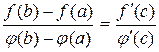 .
.
 2015-05-13
2015-05-13 376
376








