Теорема 1. Раскрытие неопределенности вида 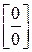 .
.
Пусть
1) функции 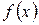 и
и 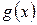 определены в промежутке
определены в промежутке 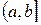 ;
;
2) 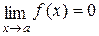 ,
, 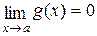 ;
;
3) существуют в промежутке 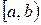 конечные производные
конечные производные 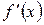 и
и 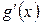 .
.
Тогда, если существует предел (конечный или бесконечный) 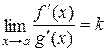 , то существует и
, то существует и 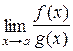 , причем
, причем
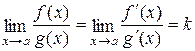 .
.
Теорема 2. Раскрытие неопределенности вида 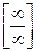 .
.
Пусть
1) функции 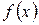 и
и 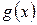 определены в промежутке
определены в промежутке 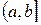 ;
;
2) 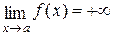 ,
, 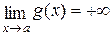 ;
;
3) существуют в промежутке 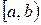 конечные производные
конечные производные 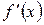 и
и 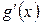 , причем
, причем 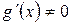 .
.
Тогда, если существует предел (конечный или бесконечный) 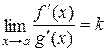 , то существует и
, то существует и 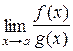 , причем
, причем
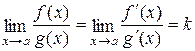 .
.
Теоремы 1 и 2 верны и в том случае, если 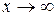 ,
, 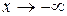 ,
, 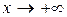 ,
, 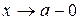 ,
, 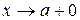 .
.
Для раскрытия неопределенностей вида 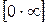 преобразуем соответствующее произведение
преобразуем соответствующее произведение 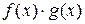 , где
, где 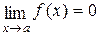 и
и 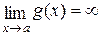 , в частное
, в частное 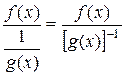 (тип
(тип 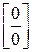 ) или
) или 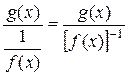 (тип
(тип 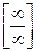 ).
).
В случае неопределенности вида 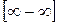 следует преобразовать соответствующую разность
следует преобразовать соответствующую разность 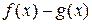 , где
, где 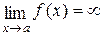 и
и 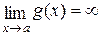 , в произведение
, в произведение 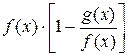 и раскрыть неопределенность
и раскрыть неопределенность 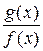 . Если
. Если 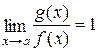 , то приводим выражение к виду
, то приводим выражение к виду 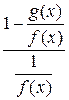 (тип
(тип 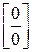 ).
).
Неопределенности вида 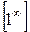 ,
, 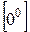 ,
, 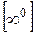 раскрывают с помощью предварительного логарифмирования и нахождения предела логарифма степени
раскрывают с помощью предварительного логарифмирования и нахождения предела логарифма степени 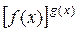 .
.
 2015-05-13
2015-05-13 1679
1679








