Пусть функция 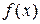 имеет в точке
имеет в точке 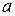 и некоторой ее окрестности производные до
и некоторой ее окрестности производные до 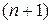 порядка включительно. Пусть
порядка включительно. Пусть 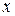 – любое значение аргумента из указанной окрестности,
– любое значение аргумента из указанной окрестности, 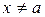 . Тогда между точками
. Тогда между точками 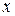 и
и 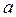 найдется точка x такая, что справедлива формула Тейлора
найдется точка x такая, что справедлива формула Тейлора
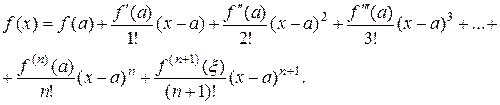
Последнее слагаемое в формуле Тейлора называется остаточным членом в форме Лагранжа и обозначается 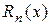 .
.
Так как точка x лежит между 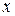 и
и 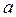 , то найдется число
, то найдется число 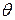 из интервала
из интервала 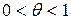 такое, что
такое, что 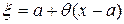 и остаточный член примет вид
и остаточный член примет вид
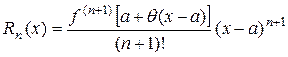 .
.
Формулу Тейлора при 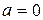 называют формулой Маклорена:
называют формулой Маклорена:
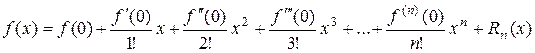 .
.
В этом случае остаточный член в форме Лагранжа примет вид:
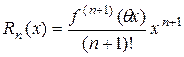 ,
,
где 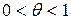 .
.
 2015-05-13
2015-05-13 451
451








