Пусть 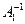 и
и 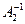 - обратные матрицы для А, тогда
- обратные матрицы для А, тогда
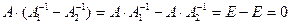
Умножим слева на 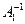 последнее выражение, получим
последнее выражение, получим
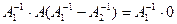 ,
,
Так как 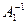 А=Е, то
А=Е, то 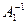 -
- 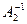 =0 или
=0 или 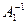 =
= 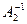
Алгоритм построения обратной матрицы:
1. Найдем Δ - определитель матрицы А. Если Δ 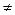 0, то А-1 существует, в противном случае обратная матрица не существует
0, то А-1 существует, в противном случае обратная матрица не существует
2. Найдем все алгебраические дополнения элементов матрицы А, то есть: Аij= 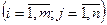
3. Запишем обратную матрицу:
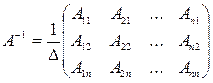
(Обратите внимание, что матрица из алгебраических дополнений транспонирована).
Упражнения. Покажите, что:
1. А·А-1=Е и А-1·А=Е
2. (А-1)-1=А
3. (А·В)-1=В-1·А-1
Пример 10. Найти матрицу, обратную для матрицы 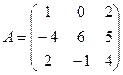 .
.
Решение. Найдем определитель матрицы А:
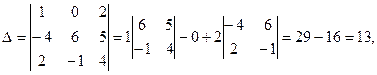
определитель не равен нулю, следовательно, обратная матрица существует Найдем все алгебраические дополнения:
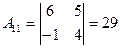 ;
; 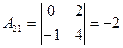 ;
; 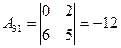 ;
;
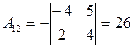 ;
; 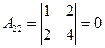 ;
; 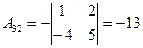 ;
;
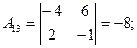
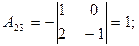
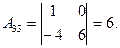
Итак, обратная матрица имеет вид: 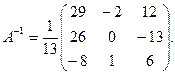
 2015-05-13
2015-05-13 736
736








