Решение. а) А - квадратная матрица, найдем ее определитель

а) А - квадратная матрица, найдем ее определитель:

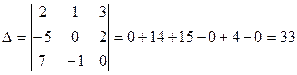
Так как минор третьего порядка не равен нулю, то rang А = r = 3.

б) Выполним элементарные преобразования над строками матрицы В:

все элементы первой строки умножим на (-1) и прибавим к соответствующим элементам второй строки. Затем сложим последние две строки, Получим:

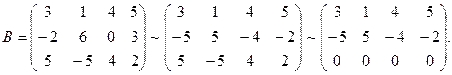
Очевидно, что все миноры третьего порядка будут равны нулю. Найдем минор второго порядка, отличный от нуля.

например,

Таким образом, rang В = 2.

СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ