Система вида:
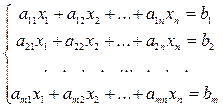
называется неоднородной системой т линейных уравнений с п неизвестными.
Здесь х1 ,..., хп - неизвестные величины,
Аij - коэффициенты системы,
bj, - свободные члены 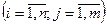
Совокупность п чисел 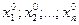 которые обращают каждое уравнение системы в тождество, называется решением системы.
которые обращают каждое уравнение системы в тождество, называется решением системы.
Если существует хотя бы одно решение, то система называется совместной, в противном случае - несовместной.
Совместная система называется определенной, если решение единственно, в противном случае - неопределенной.
Если все свободные члены bi = 0 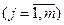 , то система называется однородной.
, то система называется однородной.
Однородная система всегда совместна, так как она имеет решение хj = 0 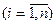 , это решение называют тривиальным.
, это решение называют тривиальным.
Запишем систему в матричной форме:
АХ=В,
где матрица 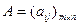 , составленная из коэффициентов системы, называется основной матрицей системы:
, составленная из коэффициентов системы, называется основной матрицей системы:
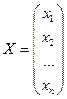 - матрица неизвестных,
- матрица неизвестных, 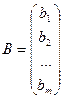 - матрица свободных членов
- матрица свободных членов
Если к матрице системы А присоединить столбец свободных членов, то получим так называемую расширенную матрицу системы, обозначим её
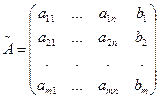 .
.
 2015-05-13
2015-05-13 317
317








