Решение. Найдем определитель основной матрицы системы

Найдем определитель основной матрицы системы:

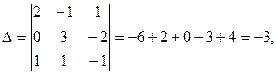
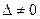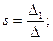
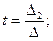
, следовательно, система имеет единственное решение.Найдем его по формулам Крамера: 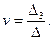где

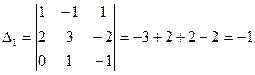
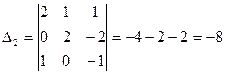
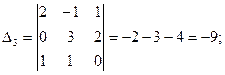
итак, ;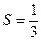

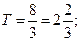
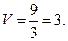
2) Матрица А - вырождена, то есть А = detA = 0.

Тогда ее ранг r(А) = r < п.

Условие совместности тоже выполнено, так как ранг расширенной матрицы 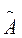равен r: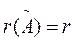

Как найти и записать решения системы в этом случае?

Пусть базисный минор матрицы А, порядок которого равен r, находится в левом верхнем углу. В этом случае п-r уравнений, коэффициенты которых не входят в базисный минор, будут линейными комбинациями первых уравнений и могут быть отброшены.

Тогда система имеет следующий вид:

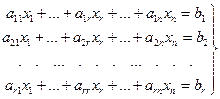
Перепишем систему, оставив слева только r слагаемых в каждом уравнении:

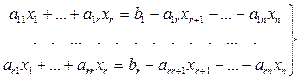
x₁ , x₂, …, x_r называют базисными переменными,

x_r+1, …, x_n называют свободными переменными.

Если выразить базисные переменные в общем виде через свободные, то получим общее решение системы. Если в этом общем решении придавать свободным переменным конкретные числовые значения, то получим частное решение системы.

Таким образом, в этом случае, когда r(А) = r( 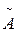) < п, система имеет бесчисленное множество решений (пример 16).