Рассмотрим неоднородную систему т уравнений с n неизвестными
АХ=В, где 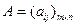
Выпишем расширенную матрицу системы:
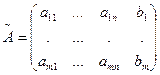 ,
,
с помощью эквивалентных преобразований над строками приведем эту матрицу к треугольному или трапециидальному виду. Решая систему уравнений, соответствующую полученной после преобразований матрице, находим единственное (пример 15) или общее (пример 16) решение данной системы.
Пример 15. Исследовать на совместность и решить систему методом Гаусса:
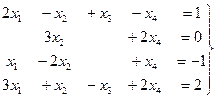 .
.
Решение. Найдем ранг расширенной матрицы системы, выполнив эквивалентные преобразования:
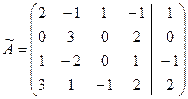 ~
~ 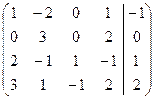 ~
~
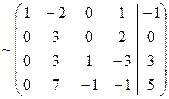 ~
~ 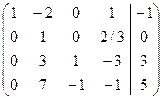 ~
~
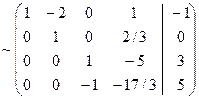 ~
~ 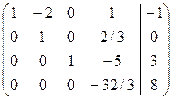 .
.
Очевидно, что r(А) = r( 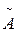 )=4, следовательно, система совместна
)=4, следовательно, система совместна
Очевидно, что r(А) = r( 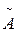 )=4, следовательно, система совместна, причем имеет единственное решение. Запишем систему, соответствующую последней матрице:
)=4, следовательно, система совместна, причем имеет единственное решение. Запишем систему, соответствующую последней матрице:
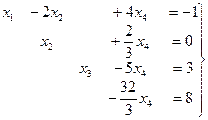
Находим значения неизвестных:
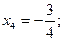
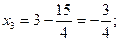
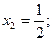
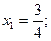
Итак, решение системы:
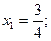
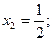
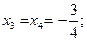
Пример 16. Исследовать на совместность и найти общее решение системы
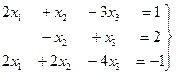 .
.
Решение.
Найдем ранг расширенной матрицы системы:
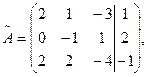 для этого из первой строки вычтем третью,
для этого из первой строки вычтем третью,
получим:
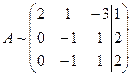 ~
~ 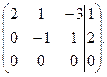
Очевидно, что r(А) = r( 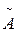 ) =2
) =2
Следовательно, система совместна. Здесь r=2, n=3, так как r<n, то система имеет бесчисленное множество решений. Найдем общее решение системы. Запишем систему, полученную после выполнения эквивалентных преобразований над расширенной матрицей системы:
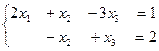 или
или 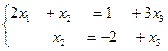 ,
,
где x1, x2 - базисные переменные,
x3 - свободная переменная.
Из первого уравнения найдем:
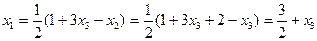 .
.
Итак, общее решение имеет вид: 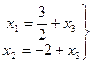
 2015-05-13
2015-05-13 332
332








