Прямая на плоскости

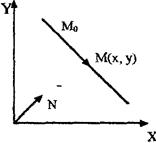
Постановка задачи Даны точка М_о (x₀, y₀) и вектор 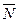(A, В) Написать уравнение прямой l, перпендикулярной вектору 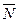и проходящей через точку M₀.

Точка M(x,y) - текущая точка прямой l.

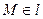тогда и только тогда, когда

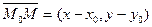и 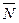(A, В) - ортогональны,

следовательно скалярное произведение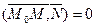

или А(x-x₀)+B(y-y₀)= 0

Итак, получили уравнение прямой, проходящей через точку M₀ и перпендикулярной .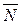

Вектор 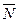называется нормальным вектором прямой.

Последнее уравнение запишем в виде

Ax+By+D=0 - оно называется общим уравнением прямой.

Другие виды уравнений прямой на плоскости:

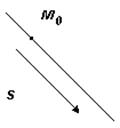
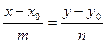- уравнение прямой, проходящей через точку М₀ (х₀, у₀) и параллельной вектору 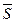(m, n).

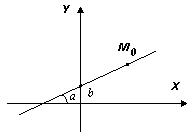
у = kx + b - уравнение прямой с угловым коэффициентом к,

где k = tg ,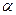

b - отрезок, отсекаемый прямой на оси OY.

у - у_о = k(x - х_о)

- уравнение прямой с угловым коэффициентом k, проходящей через точку М₀(х₀, у₀)

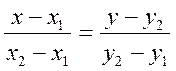
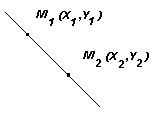
- уравнение прямой, проходящей через две точки M₁(x₁, y₁) и M₂(x₂,y₂).

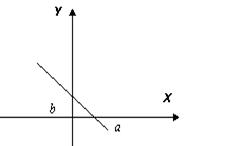
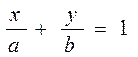- уравнение прямой в отрезках.

Между всеми этими уравнениями существует связь, то есть, если задана прямая одним из уравнений, то можно перейти к любому из перечисленных видов.

Пример 23. Написать различные виды уравнений прямой, проходящей через две точки М₁(2, 0); М₂(0, 3).