Непараметрическая статистика Манна-Уитни

(применяется при малых выборок)

Критерий применяется для проверки идентичности двух совокупностей.

Пусть взята одна выборка объемом n (символ x), выборка объема m (символ у). Предполагаем, что обе выборки взяты из одного ансамбля. Затем (n+m) наблюдений записываются в порядке возрастания, и при этом фиксируется ранг или номер позиции.

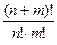- общее количество возможных структур.

Рассчитаем ранги:

R₁ – сумма рангов символа (x)

R₂ – сумма рангов символа (y)

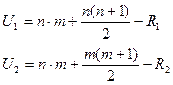
Рассчитывается по таблице в зависимости от α, m, n. Значение u(α, m, n). Среди двух статистик U₁ и U₂ выбирается наименьшее значение и сравнивается с табличным значением. Н_о отвергается, если меньшее значение меньше табличного.

12.Планирование эксперимента. Основные понятия.

- Активный эксперимент
- Пассивный эксперимент
Основная идея активного эксперимента - добиться требуемых свойств, выбирая условия проведения эксперимента.
1. План эксперимента X
1 £ j £ n 1 £ i £ N
n - число факторов, N - число экспериментов
xi= (x1i, x2i,..., xni)¢
x11, x21,..., xn1
X = xji= x12, x22,..., xn2
......
x1N, x2N,..., xnN
2. Центр плана

.. +1, -1
..
3. Центральный план
- это план, в котором центр расположен в начале координат.

4. Область определения. Нормированные переменные.

Пусть
xj*- реальные факторы
xj- нормированные факторы
-1£ xj£ 1 1£ j £ n n - факторы
Надо определить xj*min и xj*max
xj= [xj*- (xj*min+ xj*max)/2] / [(xj*max- xj*min)/2]
5. Матрица M = F¢F
y = a0+ a1x1+ a2x2+... + anxn

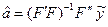
1 план
1 экспе-
f = 1 римен-
1 та
М - информационная матрица плана X размерности (k+1)*(k+1)
det(A-l I) = 0 где l- корни характеристического уравнения.
M=(Матрица у которой на диогонале числа, а все остальное нули)

План X, которому соответствует диагональная информационная матрица, называется ортогональным.
Если при применении МНК какие-либо коэффициенты а оказываются незначимыми, то в общем случае необходимо произвести перерасчет коэффициентов для новой модели.

Если использовался критерий ортогональности плана, то замена на 0 любого коэффициента в уравнении модели не изменит оценок других коэффициентов.

Преимущества ортогонального плана:
а) упрощение вычислений
б) независимые коэффициенты оценок

6. Свойство ротатабельности
План X является ротатабельным, если дисперсия оценки 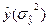зависит только от расстояния точки x от центра плана.

Пример Пусть модель y(a,x) = a0+ a1x1+ a2x2+... + anxn
x0= 0 - центр плана
M = 4I3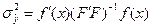



f(x) = (1, x1, x2)

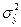= (1, x1, x2)*(1/4)I3 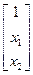= (1/4)(1+ x12+ x22) =

= (1/4)(1+r2)
Дисперсия всех равноудаленных точек одинакова.

7. План X называется ненасыщенным, если N > k+1;
насыщенным, если N = k+1

8. Критерий планирования эксперимента.
План эксперимента зависит от выбранного критерия. Критерий в основном определяет либо требования к модели, либо требования к точности.
Кроме критериев ортогональности и ротатабельности назовем критерии А-оптимальности и Д-оптимальности.
Критерий А-оптимальности требует такого выбора плана X, при котором матрица C имеет минимальный след (т.е. сумма диагональных элементов минимальна). Практически это означает минимизацию средней дисперсии оценок коэффициента а.
Критерий D-оптимальности требует такого расположения точек, при котором определитель матрицы C минимален.

13.Метод Бокса- Уилсона.

Идея метода заключается в использовании метода крутого восхождения в сочетании с последовательно планируемым факторным экспериментом для нахождения оценки градиента.
Процедура состоит из нескольких повторяющихся этапов:
- построение факторного эксперимента в окрестностях некоторой точки;
- вычисление оценки градиента в этой точке по результатам эксперимента;
- крутое восхождение в этом направлении;
- нахождение максимума функции отклика по этому направлению.
Допущения:
- функция отклика непрерывна и имеет непрерывные частные производные на множестве G;
- функция унимодальная (т.е. экстремум - внутренняя точка).

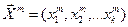
m – номер итерации

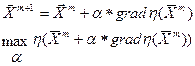
α влияет на шаг.
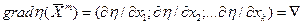- оператор Набла
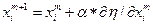Δх нужно подсчитать
Пример (на градиентный метод)
max f(x) = 4x1+ 2x2- x12- x22+5

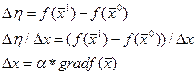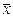= (4, 5) - исходная точка.
- общий вид
х2

х1


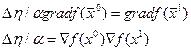
¶f/¶x1= 4 - 2x1
¶f/¶x2= 2 - 2x2
Ñf(x0) = (4-2*4, 2-2*5) = (-4, -8) - градиент в точке x0

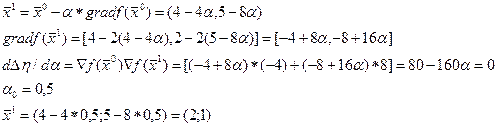
Вторая итерация

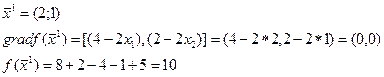
т.е. точка 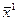- решение задачи

Оценивание градиента.
Если функция h(x1, x2,..., xk), где x1, x2,..., xk- размерные величины, то перейдем к безразмерному виду: f(x1, x2,..., xk), где x1, x2,..., xk- безразмерные величины.
Разложим эту функцию в ряд Тейлора в точке 0.


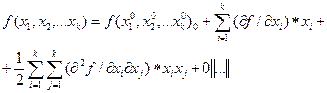
Для линейной зависимости.
f(x1, x2,..., xk) = a0+ a1x1+ a2x2+...+ akxk
где ai= ¶f/¶xi i = 1…k i ¹ 0
a0= f(x10, x20,..., xk0)0

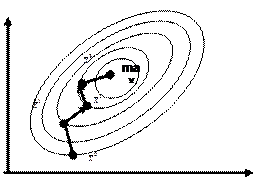
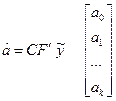- из регрессионной модели 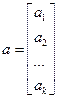- из разложения в ряд Тейлора
Проведя факторный эксперимент и рассчитав коэффициент линейной множественной регрессионной модели, мы получаем возможность оценить компоненты градиента.

14. Задача классификации. Дискриминантный анализ.
Цель дискриминантного анализа – получение правил для классификации многомерных наблюдений в одну из нескольких категорий или совокупностей. Число классов известно заранее.

Дискриминация в две известные совокупности.

Рассмотрим задачу классификации одного многомерного наблюдения х = (х1,х2,…хр)/в одну из двух совокупностей. Для этих совокупностей известны р-мерные функции плотностей 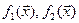Т.е. известны как форма плотности, так и ее параметры. Напомним, что если в одномерном случае параметры нормального распределения задаются двумя скалярными величинами (мат. ожиданием и дисперсией), то в многомерном случае первым параметром служит вектор мат. ожиданий, а вторым – ковариационная матрица.

Предположим, что р(1) и р(2) = 1-р(1) априорные вероятности появления наблюдения х из совокупностей 1 и 2. Тогда по теореме Байеса апостериорная вероятность того, что наблюдение х принадлежит совокупности 1 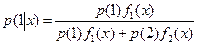а апостериорная вероятность для х принадлежать совокупности 2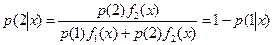

Классификация может быть осуществлена с помощью отношения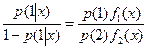
Объект относим к классу 1, если это отношение больше 1, т.е. р(1 ׀ х)>1/2, и ко второму классу, если это отношение меньше 1. Такая процедура минимизирует вероятность ошибочной классификации. При введении функции штрафа (потерь): с(2 ׀ 1) – цена ошибочной классификации наблюдения из совокупности 1 в класс 2, а с(1 ׀ 2) -
цена ошибочной классификации наблюдения из 2 в класс 1, решающее правило принимает вид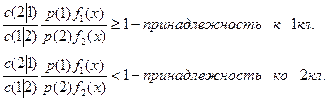
Итак, суть дискриминантного анализа состоит в следующем. Пусть известно о существовании двух или более генеральных совокупностей и даны выборки из каждой совокупности. Задача заключается в выработке основанного на имеющихся выборках правила, позволяющего приписать некоторый новый элемент к правильной генеральной совокупности, когда нам заведомо неизвестно о его принадлежности.
Суть дискриминантного анализа – разбиение выборочного пространства на непересекающиеся области. Разделение происходит с помощью дискриминантных функций. Число дискриминантных функций равно числу совокупностей. Элемент (новый) приписывается той совокупности, для которой соответствующая дискриминантная функция при подстановке выборочных значений имеет максимальное значение.

Пример задачи.

В таблице приведены результаты 4 типов измерений над 5 представителями от каждой из 3 разновидностей объектов. Измерялись величины: х1– длина объекта, х2– ширина, х3– высота, х4– масса
Методом дискриминантного анализа требуется построить совокупность линейных функций, с помощью которых любой вновь появившийся объект можно отнести в группу, к которой он действительно принадлежит. Предполагается, что к одной из 3 групп объект обязательно принадлежит (т.е. все группы образуют полное пространство), но заранее неизвестно к какой именно.
Xijk- входной вектор, содержащий данные; i – индекс-номер наблюдений i=1...5, i=1…nk; nk- размер выборки в к-й группе; j – номер переменной j=1…M, j=1…4; k- номер класса (группы) k=1…3, k=1…K
К – число групп;

Порядок счета Для каждой группы к = 1…К вычисляются

1.среднее арифметическое переменных (среднее арифметическое по каждому столбцу)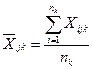

2.определяем сумму произведений отклонений от среднего значения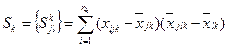

l, j=1…M
пусть при к = 1 S12=(5,1-4,86)(3,5-3,28)+(4,9-4,86)(3-3,28)+…
3. ковариационная матрица состоит из элементов, которые вычисляются по следующей формуле

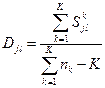где К – число групп. Т.е. для каждой группы строится ковариационная матрица, а потом объединенная. Размер 4х4. Складываем S12 для всех трех групп и делим на ∑nk– K=15-3

4. Вычисляем обратную к объединенной ковариационной матрице (метод Жордана-Гаусса)

5. Вычисляем общие средние для всех переменных 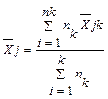j=1,M k=1,k; 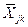- среднее j–й переменной в каждой к-й группе. Например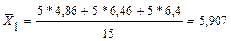

6. Вычисляем обобщенную D2статистику (расстояние Махалонобиса)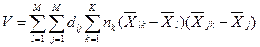

dlj– элемент обращенной ковариационной матрицы

V используют как критерий χ2(с допущением нормальности) с M(k-1) степенями свободы для проверки гипотезы, что средние значения данных переменных одинаковы во всех «к» группах.
Проанализируем расстояние Махаланобиса =некий числитель/ объединен. ковариац. м-цу. Числитель – сумма по группам произведений расстояний между средним арифметическим переменной по всем данным и средним арифметическим в данном классе, а знаменатель – внутригрупповые расстояния. В нашем примере V=5865,4 можно использовать как χ2с r = М(К-1)=4(3-1)=8 степенями свободы для проверки гипотезы, что средние значения во всех k группах одинаковые.

Если V>Vтабл. (Vтабл.®χ2), то вероятность подтверждения этой гипотезы ничтожна, т.е. средние значения в классах разные.

7. Считаем дискриминантные функции f1, f2,….fk 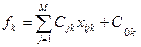, где 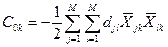- константы, k=1,K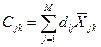
Для каждого i – го наблюдения в каждой группе вычисляются значения дискриминантных функций.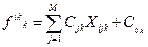
В нашем примере дискриминантные функции для трех групп F1= -443,4+105,5x1+144,1x2-55,1x3-105,4x4
F2= -766,9-3,79х1+118,1х2+211,2х3+176,9х4; F3= -1253,6-63,1х1+101,9х2+342,1х3+316,3х4
Рассмотрим объект с характеристиками х1=5,8 х2=2,7 х3=5,1 х4=1,9 (это 2-е наблюдение 3 группы)
Вычислим для него Fi: F1=75,8 F2=943 F3=1001,3; Так как наибольшее значение F3, то объект следует отнести к 3 группе

8. Оцениваем достоверность. Для этого считаем вероятность, соответствующую наибольшей дискриминантной функции 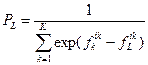; fL– значение наибольшей дискриминантной функции
L – индекс наибольшей дискриминантной функции
В нашем примере вычислим для каждого i-го наблюдения в каждой из k групп значения дискриминантных функций fkikk=1..3.
Среди этих значений выбирают максимальное fmik=max(f1ik,f2ik,f3ik).
В нашем случае fm23= f3, L=3.
Считаем критерий достоверности, т.е. вероятность pL, соответствующую наибольшей дискриминантной функции
f1-f3= 75,8-1001,3 = -925,5
f2-f3= 943-1001,3 = -58,3
p3=1/(е-925,5+е-58,3+1) =1
pLпоказывает с какой уверенностью мы можем отнести наблюдаемый объект в группу, на которую указывает рез-т дискриминации. Чем больше разница fk-fL, тем сильнее различаются значения дискриминантных функций, тем больше вероятность