Суть метода в том, что сначала, воспользовавшись преобразованием Лапласа, переходят от оригиналов функций к их изображениям:
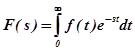 .
.
Затем с изображениями производят преобразования, а результат приводят к форме, удобной для совершения обратного преобразования Лапласа:
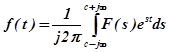
Изображение функции времени является функцией некоторой комплексной величины 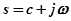 . Вещественная часть ее представляет собой так называемую абсциссу абсолютной сходимости, которая выбирается так, чтобы удовлетворялось неравенство:
. Вещественная часть ее представляет собой так называемую абсциссу абсолютной сходимости, которая выбирается так, чтобы удовлетворялось неравенство:
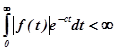 .
.
Для большинства функций в теории автоматического регулирования абсцисса абсолютной сходимости равна нулю, т. е. с=0. Поэтому для этих функций 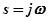 .
.
Дифференциальные уравнения движения систем в операторном методе записываются в символической форме. При этом используется оператор Лапласа: 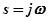 .
.
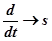 ;
; 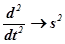 ;
; 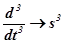 ;
;
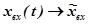 ;
; 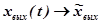 .
.
Рассмотрим пример представления дифференциального уравнения в операторной форме:
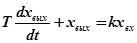 ;
;
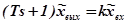 ;
;
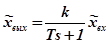 .
.
 2015-05-13
2015-05-13 411
411








